Advertisements
Advertisements
प्रश्न
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
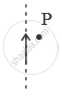
उत्तर
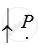
`therefore` By Biot savart’s law
`vec(B) = ∫ vec (dB) = mu_0/(4pi) ∫ (I vec(dl) xx vec(r))/r^3`
The magnetic field created by a current carrying wire is radial magnetic field.
APPEARS IN
संबंधित प्रश्न
An alpha particle is projected vertically upward with a speed of 3.0 × 104 km s−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the α-particle.
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that ______.
The magnetic field at any point on the axis of a current element is ______
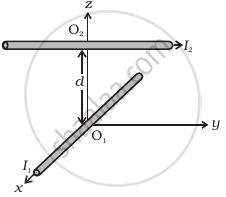
Two long wires carrying current I1 and I2 are arranged as shown in figure. The one carrying current I1 is along is the x-axis. The other carrying current I2 is along a line parallel to the y-axis given by x = 0 and z = d. Find the force exerted at O2 because of the wire along the x-axis.
Two identical circular loops P and Q, each of radius R carrying current I are kept in perpendicular planes such that they have a common centre O as shown in the figure.
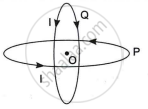
Find the magnitude and direction of the net magnetic field at point O.
