Advertisements
Advertisements
प्रश्न
Two identical circular loops P and Q, each of radius R carrying current I are kept in perpendicular planes such that they have a common centre O as shown in the figure.
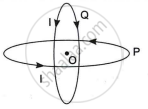
Find the magnitude and direction of the net magnetic field at point O.
उत्तर
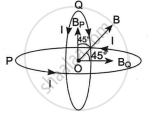
In the P coil, the current is in an anticlockwise direction. So the magnetic field (BP) will be in the direction shown.
Similarly, in Q the direction of magnetic field BQ will be shown (from Flemings left-hand rule) the resultant of BP and BQ will be B.
So `B = sqrt(B_P^2 + B_Q^2)`
BP = BQ
because both the coil has the same current and the same radius.
`B = sqrt(B_P^2 + B_P^2) = sqrt2B_P`
∵ `B_P = (mu_0I)/(2R)`
`B = sqrt2((mu_0I)/(2R))`
⇒ B = `(mu_0I)/(sqrt2R)`
The net magnetic field is oriented to both fields at 45°.
APPEARS IN
संबंधित प्रश्न
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State Biot Savart law.
Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
A circular loop of radius 0.3 cm lies parallel to much bigger circular of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with the bigger loop is ______.
Biot-Sawart law indicates that the moving electrons (velocity `overset(->)("v")`) produce a magnetic field B such that
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
