Advertisements
Advertisements
प्रश्न
A straight wire carrying a current of 5 A is bent into a semicircular arc radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the center of the arc

उत्तर

The magnetic field at the center of the arc due to straight elements is given by,
`"B" = int mu_°/(4pi) ("i" vec"dl" xx vec"r")/("r"^3)`
For straight elements PQ and RS, `vec"dl" || vec"r"` for the center of the arc.
`∵ vec"dl" xx vec"r" = 0`
⇒ B = 0 .......(Due to PQ & RS)
The magnetic field at the center O, due to the semicircular arc is half of the magnetic field produced by a full circular coil at the center.
`"B" = 1/2 ((mu_°"i")/"2R")`
`"B" =(mu_°"i")/"4R"`.........( Due to semi circular arc)
i = 5 A & R = 2 × 10-2 m
`∴"B" = (4pi xx 10^-7 xx 5)/(4 xx 2 xx 10^-2) = 2.5 pi xx 10^-5 "T"`
⇒ B = 2.5 π × 10-5 T
APPEARS IN
संबंधित प्रश्न
State Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
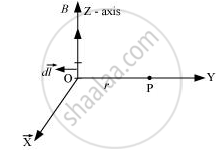
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
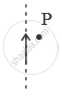
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
Derive the expression for the magnetic field due to a current-carrying coil of radius r at a distance x from the center along the X-axis.
A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

Biot-Sawart law indicates that the moving electrons (velocity `overset(->)("v")`) produce a magnetic field B such that
The magnetic field at any point on the axis of a current element is ______
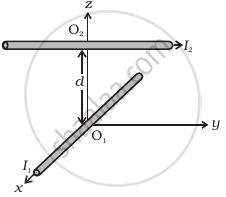
Two long wires carrying current I1 and I2 are arranged as shown in figure. The one carrying current I1 is along is the x-axis. The other carrying current I2 is along a line parallel to the y-axis given by x = 0 and z = d. Find the force exerted at O2 because of the wire along the x-axis.
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
