Advertisements
Advertisements
प्रश्न
Derive the expression for the magnetic field due to a current-carrying coil of radius r at a distance x from the center along the X-axis.
उत्तर
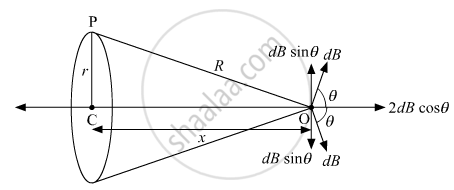
Consider a conducting element dl of the loop. The magnitude dB of the magnetic field due to dl is given by the Biot-Savart law,
`"dB" = mu_°/(4pi) ("i"|vec(dl) xx vec("R")|)/"R"^3 `
`"dB" = mu_° /(4pi) ("idl")/"R"^2 (vec"idl" ⊥ vec"R")`
From the above figure, we can see, R2 = r2 +x2
`"dB" = mu_° /(4pi) xx "idl"/("r"^2 + "x"^2)`
The direction of the magnetic field is shown in the figure, as we can see, only cosine component of the magnetic field will play a role here, all the sine component will get cancel out to give a zero net value.
`"dB"_"net" = mu_°/(4pi) xx "idl"/(("r"^2 + "x"^2)) xx costheta`
`"dB"_"net" = mu_°/(4pi) xx "idl"/(("r"^2 + "x"^2)) xx "r"/(sqrt("r"^2+"x"^2)) `
`"dB"_"net" = (mu_° "idl")/(4pi) "r"/(("r"^2 + "x"^2)^(3//2))`
∵ dl = rdθ
⇒ `"B"_"net" = (mu_°"i")/(4pi) ("r"^2 int_0^(2pi) "d"theta)/(("r"^2 + "x"^2)^(3//2)) = (mu_°"ir"^2)/(2("r"^2+ "x"^2)^(3//2))`
⇒ `"B"_"net" = (mu_°"ir"^2)/(2("r"^2+ "x"^2)^(3//2))`
⇒ `vec("B"_"net") = (mu_°"ir"^2)/(2("r"^2+ "x"^2)^(3//2)) hat"i"`
APPEARS IN
संबंधित प्रश्न
Express Biot – Savart law in the vector form.
A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
A straight wire carrying a current of 5 A is bent into a semicircular arc radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the center of the arc

A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

Two identical circular loops P and Q, each of radius R carrying current I are kept in perpendicular planes such that they have a common centre O as shown in the figure.
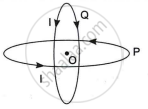
Find the magnitude and direction of the net magnetic field at point O.
