Advertisements
Advertisements
प्रश्न
Suppose the pressure at the surface of mercury in a barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
पर्याय
P1 = 0, P2 = atmospheric pressure
P1 = atmospheric pressure P2 = 0
P1 = P2 = atmospheric pressure
P1 = P2 = 0
उत्तर
P1 = 0, P2 = atmospheric pressure
The upper part of the tube contains vacuum as the mercury goes down and no air is allowed in. Thus, the pressure at the upper end, i.e., at the surface of mercury in a barometer tube is zero (P1 = 0). However, the pressure at the surface of mercury in the cup or any another point at the same horizontal plane is equal to the atmospheric pressure.
APPEARS IN
संबंधित प्रश्न
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
A one meter long glass tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end to a suction pump. Can mercury be pulled up into the pump by this process?
A satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1 m long placed in the satellite?
The three vessels shown in the following figure have same base area. Equal volumes of a liquid are poured in the three vessels. The force on the base will be
Equal mass of three liquids are kept in three identical cylindrical vessels A, B and C. The densities are ρA, ρB, ρC with ρA < ρB < ρC. The force on the base will be
Shows in the following figure a siphon. The liquid shown is water. The pressure difference PB − PAbetween the points A and B is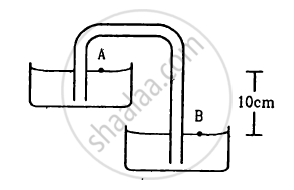
A barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be ______.
A barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
The surface of water in a water tank on the top of a house is 4 m above the tap level. Find the pressure of water at the tap when the tap is closed. Is it necessary to specify that the tap is closed?
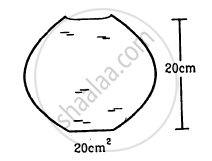
A glass full of water has a bottom of area 20 cm2, top of area 20 cm2, height 20 cm and volume half a litre.
(a) Find the force exerted by the water on the bottom.
(b) Considering the equilibrium of the water, find the resultant force exerted by the sides of the glass on the water. Atmospheric pressure = 1.0 × 105 N/m2. Density of water 1000 kg/m3 and g = 10 m/s2. Take all numbers
to be exact.
Water is filled in a rectangular tank of size 3 m × 2 m × 1 m. (a) Find the total force exerted by the water on the bottom surface on the tank. (b) Consider a vertical side of area 2 m × 1 m. Take a horizontal strip of width δx metre in this side, situated at a depth of x metre from the surface of water. Find the force by the water on this strip. (c) Find the torque of the force calculate in part (b) about the bottom edge of this side.
(d) Find the total force by the water on this side.
(e) Find the total torque by the water on the side about the bottom edge. Neglect the atmospheric pressure and take g = 10 ms−2.
Water leaks out from an open tank through a hole of area 2 mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tanks is 0.4 m2. The pressure at the open surface and at the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. (a) Find the initial speed of water coming out of the hole. (b) Find the speed of water coming out when half of water has leaked out. (c) Find the volume of eater leaked out using a time interval dt after the height remained is h. Thus find the decrease in height dh in terms of h and dt.
(d) From the result of park (c) find the time required for half of the water to leak out.
Pressure decreases as one ascends the atmosphere. If the density of air is ρ, what is the change in pressure dp over a differential height dh?
Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the surface of the earth is p0.
