Advertisements
Advertisements
प्रश्न
Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F1 = – F2 = `- r_12/r_12^3 GM_0^2 ((m_1m_2)/M_0^2)^n` where M0 is a constant of dimension of mass r12 = r1 – r2 and n is a number. in such a case.
- the acceleration due to gravity on earth will be different for different objects.
- none of the three laws of Kepler will be valid.
- only the third law will become invalid.
- for n negative, an object lighter than water will sink in water.
Advertisements
उत्तर
a, c and d
Explanation:
Given, `F_1 = - F_2 = (-r_12)/r_12^3 GM_0^2 ((m_1m_2)/m_0^2)^n`
Acceleration due to gravity, `g = (|F|)/"mass"`
= `(GM_0^2 (m_1m_2)^n)/(r_12^2 (M_0)^(2n)) xx 1/(("mass"))`
Since. g depends upon the position vector, hence it will be different for different objects. As g is not constant, hence constant of proportionality will not be constant in Kepler's third law. Hence, Kepler's third law will not be valid.
As the force is of central nature. .....`[∵ "Force" ∝ 1/r^2]`
Hence, the first two of Kepler's laws will be valid.
For negative n, g = `(GM_0^2 (m_1m_2)^-n)/(r_12^2 (M_0)^(-2n)) xx 1/(("mass"))`
= `(GM_0^(2(1 + n)))/r_12^2 ((m_1m_2)^-n)/(("mass"))`
g = `(GM_0^2)/r_12^2 (M_0^2/(m_1m_2)) xx 1/"mass"`
As M0 > m1 or m2
g > 0, hence in this case situation will reverse i.e., an object lighter than water will sink in water.
APPEARS IN
संबंधित प्रश्न
State Kepler's law of orbit and law of equal areas.
A Saturn year is 29.5 times the earth year. How far is the Saturn from the sun if the earth is 1.50 ×108 km away from the sun?
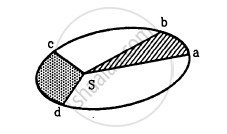
In the Following figure shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t1 and t2 be the time taken by the planet to go from a to b and from c to d respectively,
Answer the following question.
State Kepler’s law of the period.
Observe the given figure showing the orbit of a planet moving around the Sun and write the three laws related to it:
The orbit of a planet moving around the Sun
The orbit of a planet revolving around a star is _______.
The square of its period of revolution around the sun is directly proportional to the _______ of the mean distance of a planet from the sun.
State Kepler’s laws.
If the distance between the sun and the earth is made three times, then attraction between the two will ______
A planet is revolving around the sun in an elliptical orbit as shown in figure. At which point will its K.E. be maximum?
The mass and radius of earth is 'Me' and 'Re' respectively and that of moon is 'Mm' and 'Rm' respectively. The distance between the centre of the earth and that of moon is 'D'. The minimum speed required for a body (mass 'm') to project from a point midway between their centres to escape to infinity is ______.
Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon ______.
If the sun and the planets carried huge amounts of opposite charges ______.
- all three of Kepler’s laws would still be valid.
- only the third law will be valid.
- the second law will not change.
- the first law will still be valid.
A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
A planet revolving in an elliptical orbit has:
- a constant velocity of revolution.
- has the least velocity when it is nearest to the sun.
- its areal velocity is directly proportional to its velocity.
- areal velocity is inversely proportional to its velocity.
- to follow a trajectory such that the areal velocity is constant.
Choose the correct answer from the options given below:
lf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, and its areal velocity is ______.
What is one practical use of Kepler’s laws?
What is at one focus of the elliptical orbit of a planet?
The time taken by a planet to orbit the Sun depends on ______.
