Advertisements
Advertisements
प्रश्न
The 9th term of an AP is -32 and the sum of its 11th and 13th terms is -94. Find the common difference of the AP.
उत्तर
Let a be the first term and d be the common difference of the AP. Then,
a9 = - 32
⇒ a +(9-1) d= -32 [an = a + (n-1) d]
⇒ a + 8d = -32 ............(1)
Now ,
`a_11 + a_13 = -94` (Given)
`⇒ ( a +10d ) +( a + 12d) = -94`
⇒ 2a + 22d = -94
⇒ a+ 11d = -47 ...............(2)
From (1) and (2), we get
-32 -8d + 11d=-47
⇒ 3d = -47 + 32 =-15
⇒ d = -5
Hence, the common difference of the AP is - 5.
APPEARS IN
संबंधित प्रश्न
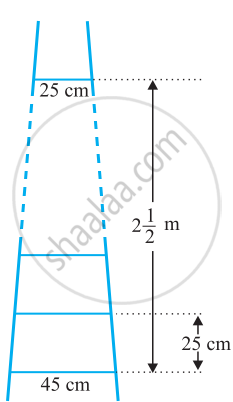
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find the sum of the first 25 terms of an A.P. whose nth term is given by an = 2 − 3n.
The 4th term of an AP is zero. Prove that its 25th term is triple its 11th term.
Choose the correct alternative answer for the following question .
In an A.P. first two terms are –3, 4 then 21st term is ...
The first and last term of an A.P. are a and l respectively. If S is the sum of all the terms of the A.P. and the common difference is given by \[\frac{l^2 - a^2}{k - (l + a)}\] , then k =
The term A.P is 8, 10, 12, 14,...., 126 . find A.P.
x is nth term of the given A.P. an = x find x .
Which term of the AP 3, 15, 27, 39, ...... will be 120 more than its 21st term?
Find the next 4 terms of the sequence `1/6, 1/4, 1/3`. Also find Sn.
If Sn denotes the sum of first n terms of an AP, prove that S12 = 3(S8 – S4)
