Advertisements
Advertisements
प्रश्न
The area between the circumferences of two concentric circles is 2464 cm2. If the inner circle has circumference of 132 cm, calculate the radius of outer circle.
उत्तर
For the inner circle :
Circumference = 2 π r = 132
2 π r = 132
`2 xx 22/7 xx "r" = 132`
`"r" = (132 xx 7)/(2 xx 22)`
r = 21 cm
Therefore, radius of inner circle = 21 cm
Area of inner ci rel e = π r2
`= 22/7 xx 21 xx 21`
= 1386 cm2
Area of outer circle = area of inner circle + area of concentric circles
= (1386 + 2464) cm2 = 3850 cm2
⇒ π r2 = 3850
⇒ R2 = `3850 xx 7/22`
⇒ R2 = 1225
⇒ R = 35 cm
Hence, radius of outer circle = 35 cm
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 7 cm. find the circumference of the circle.
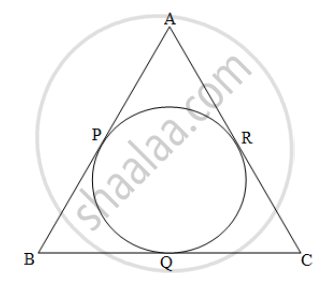
In figure, ΔABC is an isosceles triangle with perimeter 44 cm. The base BC is of length 12 cm. Side AB and side AC are congruent. A circle touches the three sides as shown in the figure below. Find the length of the tangent segment from A to the circle.
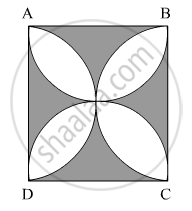
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
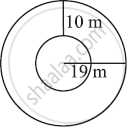
Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
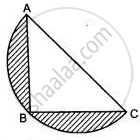
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
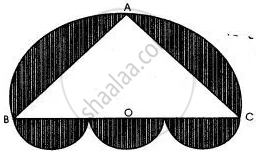
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
Find the area of circle whose circumference is 44 cm.
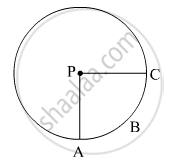
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
Find the length of the arc of a circle of diameter 42 cm which subtends an angle of 60° at the centre.
The side of a square is 10 cm. Find the area of the circumscribed circle. [π = 3.14]
In making 1000 revolutions, a wheel covers 88 km. The diameter of the wheel is
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the area of the minor and major segments.
A canvas tent is in the shape of a cylinder surmounted by a conical roof. The common diameter of the cone and the cylinder is 14 m. The height of the cylindrical part is 8 m and the height of the conical roof is 4 m. Find the area of the canvas used to make the tent.
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
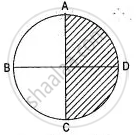
AC and BD are two perpendicular diameter of a circle ABCD. Given that the area of shaded portion is 308 cm2 calculate:
(i) The length of AC and
(ii) The circumference of circle
The diameter of a wheel is 1.4m. How many revolutions does make in moving a distance of 2.2km?
The radius of the wheel of a bus is 0.7 m. How many rotations will a wheel complete while traveling a distance of 22 km?
Formula used to find the circumference of a circle is
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where `pi = 22/7` then length of an arc is ____________.
