Advertisements
Advertisements
प्रश्न
The area of a square is 100 cm2. The circumference (in cm) of the largest circle cut of it is ______.
पर्याय
5 π
10 π
15 π
20 π
उत्तर
The area of a square is 100 cm2. The circumference (in cm) of the largest circle cut of it is 10 π.
Explanation:
Let the side of square be a cm.
Given, area of square = 100 cm2
∴ Area of square = a2
⇒ a2 = 100 cm2 ......[∵ Area of square = (side)2]
⇒ a = `sqrt(100)`
⇒ a = 10 cm
Now, for the largest circle in the square, diameter of the circle must e equal to the side of square.
∴ Diameter = Side of a square = 10 cm
⇒ 2r = 10 cm ......[∵ Diameter = 2 × radius]]
⇒ r = 5 cm
∴ Circumference of the circle = 2 πr = 2 × π × 5 = 10 π cm.
APPEARS IN
संबंधित प्रश्न
In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. Use π = `(\frac { 22 }{ 7 }).`
A horse is placed for grazing inside a rectangular field 40m by 36m and is tethered to one corner by a rope 14m long. Over how much area can it graze.
Choose the correct alternative answer for the following question.
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]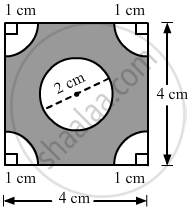
Find the perimeter of the shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.
The cost of fencing a circular field at the rate of Rs.250 per metre is Rs.55000. The field is to be ploughing at the rate of Rs.15 per m2. Find the cost of ploughing the field.
Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? (Use π = `22/7`)
The radius of a circular plot is 7.7 metres. How much will it cost to fence the plot with 3 rounds of wire at the rate of 50 rupees per metre?
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
