Question

The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation algebraically and geometrically.

Answer 1

Let the cost of 1 kg of apples be Rs x.

And, cost of 1 kg of grapes = Rs y

According to the question, the algebraic representation is

2x + y = 160

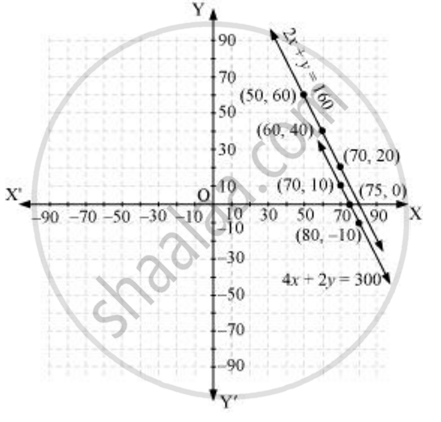
4x + 2y = 300

For 2x + y = 160

y = 160 - 2x

The solution table is

x	50	60	70
y	60	40	20

For 4x + 2y = 300,

`y = (300 - 4x)/2`

The solution table is

x	70	80	75
y	10	−10	0

The graphical representation is as follows

Answer 2

Cost per kg of apple = Rs x

Cost per kg of grapes = Rs y

Algerbraically 2x + y = 160 ...........(1)

4x + 2y = 300 or 2x + y = 150 ..........(2)

From (1) y = 160 - 2x

x	50	60
Y = 160 - 2x	60	40

From (2), y = 150 - 2x

x	50	60
Y = 150 - 2x	50	30

The graphical representation is as follow