Advertisements
Advertisements
प्रश्न
The following figure shows a part of an electric circuit. The potentials at the points a, b and care 30 V, 12 V and 2 V respectively. Find the currents through the three resistors.
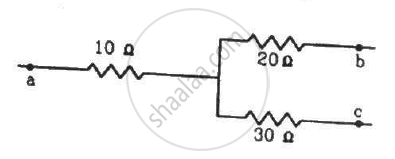
उत्तर
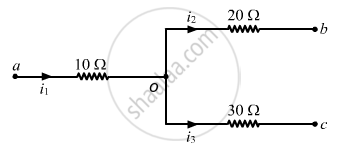
Let the potential at the point o be X volts.
From the figure,
\[i_1 = \frac{V_a - V_o}{10}\]
\[ V_a = 30V\text{ and }V_o = X\]
\[So, i_1 = \frac{30 - X}{10}\]
Similarly,
\[ i_2 = \frac{V_o - V_b}{20}\]
\[ = \frac{X - 12}{20}\]
And
\[ i_3 = \frac{V_o - V_c}{30}\]
\[ = \frac{X - 2}{30}\]
Also, from kirchoff's junction law we have:-
i1 = i2 + i3
\[\Rightarrow \frac{30 - X}{10} = \frac{X - 12}{20} + \frac{X - 2}{30}\]
\[ \Rightarrow 30 - X = \frac{X - 12}{2} + \frac{X - 2}{3}\]
\[ \Rightarrow 30 - X = \frac{3X - 36 + 2X - 4}{6}\]
\[ \Rightarrow 180 - 6X = 5X - 40\]
\[ \Rightarrow 11X = 220\]
\[ \Rightarrow X = \frac{220}{11} = 20 V\]
Thus, the currents through the three resistors are:-
\[i_1 = \frac{30 - 20}{10} = 1A\]
\[ i_2 = \frac{20 - 12}{20} = \frac{8}{20} = 0 . 4A\]
\[ i_3 = \frac{20 - 2}{30} = \frac{18}{30} = 0 . 6 A\]
