Advertisements
Advertisements
प्रश्न
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Advertisements
उत्तर
Let us consider the diagram of a spherical shell having uniform density (ρ).
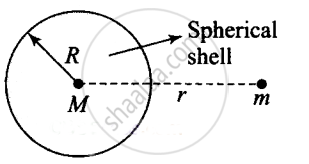
Mass of the shell = (Density) × (Volume)
`M = (ρ) xx 4/3 πR^3`
Therefore, the gravitational force between the hollow shell and point mass is`F = (GMm)/r^2` where M is the mass of the hollow spherical shell and m is the mass of point mass.
Therefore, the mass is distributed on the surface of the sphere only, then F = 0 for 0 < r < R (i.e., force inside the shell is zero)
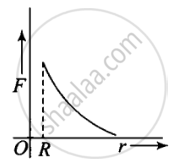
And `F = (GM)/r^2 for `r ≥ R`
The variation of F versus r is shown in the diagram. Force is maximum at the surface of shell and it is zero if r tends to infinity.
APPEARS IN
संबंधित प्रश्न
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Inside a uniform spherical shell
(a) the gravitational potential is zero
(b) the gravitational field is zero
(c) the gravitational potential is same everywhere
(d) the gravitational field is same everywhere
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
State whether the gravitational force between two masses is attractive or repulsive ?
How will the force of gravitation between two objects change if the distance between them is:
Doubled
The force of attraction between any two material objects is called __________.
A ball is thrown up with a speed of 4.9 ms-1.
Prove that the time of ascent is equal to the time of descent.
Is there a gravitational attraction between you and the book? Explain.
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
The gravitational force between two bodies is directly proportional to the product of the masses of those bodies and is ______ of the distance between them.
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
If the mass of one object is doubled and distance remains the same, the gravitational force will ______.
Ocean tides on Earth are mainly caused by ______.
For an object outside a uniform solid sphere, from where is the sphere's mass considered to act?
