Advertisements
Advertisements
प्रश्न
The length, breadth, and height of a rectangular solid are in the ratio 5: 4: 2. If the total surface area is 1216 cm2, find the length, the breadth, and the height of the solid.
उत्तर
The rectangular solid is a cuboid.
Let the length of the cuboid = 5a, breadth = 4a, and height = 2a
Total surface area of a cuboid of length l, breadth b and height h = 2(l × b + b × h + l × h)
Given,
Total surface area of the cuboid = 1216 cm2
⇒ 2(5a × 4a + 4a × 2a + 2a × 5a) = 1216 cm2
⇒ 76a2 = 1216
⇒ a = 4.
Hence, the length of the cuboid = 5a = 20 cm, breadth = 4a = 16 cm, height = 2a = 8 cm.
APPEARS IN
संबंधित प्रश्न
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs. 5 per metre sheet, sheet being 2 m wide.
Ravish wanted to make a temporary shelter for his car by making a box-like structure with tarpaulin that covers all the four sides and the top of the car ( with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m with
base dimensions 4 m × 3m?
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk?
A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm3 each are to be made. Find the number of beads that can be made from the block.
Find the surface area of a cuboid whose length = 10 cm, breadth = 12 cm, height = 14 cm.
The cost of constructing a wall 8 m long, 4 m high and 10 cm thick at the rate of Rs. 25 per m3 is
A cuboid is 8 m long, 12 m broad and 3.5 high, Find its
(i) total surface area
(ii) lateral surface area
The curved surface area and the volume of a toy, cylindrical in shape, are 132 cm2 and 462 cm3 respectively. Find, its diameter and its length.
The surface area of a cuboid formed by joining face to face 3 cubes of side x is 3 times the surface area of a cube of side x.
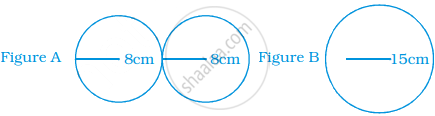
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?