Advertisements
Advertisements
प्रश्न
The length of a chord of a circle of 16.8 cm, radius is 9.1 cm. Find its distance from the centre.
बेरीज
उत्तर
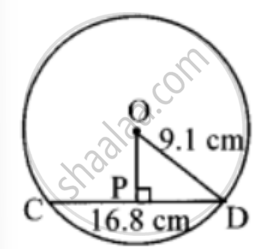
Let CD be the chord of the Circle with centre O.
Draw seg OP ⊥ chord CD
∴ l(PD) = `(1/2) l("CD")` …[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴ l(PD) = `(1/2) xx 16.8` …[l(CD) = 16.8 cm]
∴ l(PD) = 8.4 cm …(i)
∴ In ∆OPD, m∠OPD = 90°
∴ [l(OD)]2 = [l(OP)]2 + [l(PD)]2 ….. [Pythagoras theorem]
∴ (9.1)2 = [l(OP)]2 + (8.4)2 … [From (i) and l(OD) = 9.1 cm]
∴(9.1)2 – (8.4)2 = [l(OP)]2
∴(9.1 + 8.4) (9.1 – 8.4) = [l(OP)]2 …[∵ a2 – b2 = (a + b) (a – b)]
∴17.5 × (0.7) = [l(OP)]2
∴ 12.25 = [l(OP)]2
i.e., [l(OP)]2 = 12.25
∴ l(OP) = `sqrt12.25` …[Taking square root of both sides]
∴ l(OP) = 3.5 cm
shaalaa.com
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
