Advertisements
Advertisements
प्रश्न
The magnetic moment vectors µs and µl associated with the intrinsic spin angular momentum S and orbital angular momentum l, respectively, of an electron are predicted by quantum theory (and verified experimentally to a high accuracy) to be given by:
µs = –(e/m) S,
µl = –(e/2m) l
Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
उत्तर
The magnetic moment associated with the orbital angular momentum is valid with classical mechanics.
The magnetic moment associated with the orbital angular momentum is given as
µl = `-("e"/(2"m")) "l"`
For current i and area of cross-section A, we have the relation:
Magnetic moment
µl = iA ……….(1)
Where,
e = Charge of the electron
r = Radius of the circular orbit
T = Time taken to complete one rotation around the circular orbit of radius r
Orbital angular momentum, l = mvr
L = `"m" xx (2π"r")/"T" xx "r"` ……….(2)
Where,
m = Mass of the electron
v = Velocity of the electron
r = Radius of the circular orbit
Dividing equation (1) by equation (2), we get:
`(µ_"l")/"T" = -("e"/(2"m"))`
µl = `-("e"/(2"m")) "l"`
APPEARS IN
संबंधित प्रश्न
A circular coil of 300 turns and average area 5 * 10-3m2 carries a current of 15A. Calculate the magnitude of magnetic moment associated with the coil.
Show that the orbital magnetic dipole moment of a revolving electron is `(eVr)/2`
An electron in an atom revolves around the nucleus in an orbit of radius 0.53 Å. If the frequency of revolution of an electron is 9 x109 MHz, calculate the orbital angular momentum
[Given : Charge on an electron = 1.6 x 10–19 C; Gyromagnetic ratio = 8.8 x 1010 C/kg; π = 3.142]
The electron in the hydrogen atom is moving with a speed of 2.3x106 m/s in an orbit of radius 0.53 Å. Calculate the period of revolution of the electron. (Π = 3.142)
Do two distinct poles actually exist at two nearby points in a magnetic dipole?
A circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
A circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the loop is in ______.
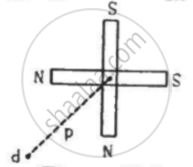
Two short magnets of equal dipole moments M are fastened perpendicularly at their centre in the Figure . The magnitude of the magnetic field at a distance d from the centre on the bisector of the right angle is
A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.04 G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (me = 9.11 × 10–31 kg).
