Advertisements
Advertisements
प्रश्न
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction.
उत्तर
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
The sum of the numerator and denominator of the fraction is 3 less than twice the denominator. Thus, we have
`x+y=2y-3`
`⇒ x+y-2y+3=0`
`⇒ x-y+3=0`
If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Thus, we have
` x-1=1/2(y-1)`
`⇒ (x-1)/(y-1)=1/2`
`⇒ 2(x-1)=y-1`
`⇒ 2x -2 =y-1`
`⇒ 2x -y -1=0`
So, we have two equations
`x-y+3=0`
`2x-y-5=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx(-1)-(-1)xx3)=(-y)/(1xx(-1)-2xx3)=1/(1xx(-1)-2xx(-1))`
`⇒ x/(1+3)=(-y)/(-1-6)=(1)/(-1+2)`
`⇒ x/4 = (-y)/-7 =1/1`
`⇒ x/4=y/7=1`
`⇒ x = 4,y=7`
Hence, the fraction is `4/7`
APPEARS IN
संबंधित प्रश्न
Solve `\frac{1}{x+y}+\frac{2}{x-y}=2\text{ and }\frac{2}{x+y}-\frac{1}{x-y}=3` where, x + y ≠ 0 and x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`4/x + 3y = 14`
`3/x - 4y = 23`
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
Formulate the following problems as a pair of equations, and hence find their solutions:
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current
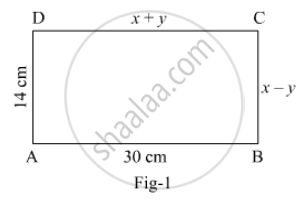
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
If 2 is added to the numerator of a fraction, it reduces to 1/2 and if 1 is subtracted from the denominator, it reduces to 1/3. Find the fraction.
A father is three times as old as his son. After twelve years, his age will be twice as that of his son then. Find the their present ages.
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B?
Ten years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages.
Asha has only ₹1 and ₹2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹75, then the number of ₹1 and ₹2 coins are, respectively.
