Advertisements
Advertisements
प्रश्न
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. Find the fraction.
उत्तर
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
The sum of the numerator and denominator of the fraction is 12. Thus, we have
`x+y=12`
`⇒ x+y-12=0`
If the denominator is increased by 3, the fraction becomes `1/2`. Thus, we have
`x/(y+3)=1/2`
`⇒ 2x=y+3`
`⇒ 2x -y -3=0`
So, we have two equations
`x+y-12=0`
`2x-y-3=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/(1xx(-3)-(-1)xx(-12))=(-y)/(1xx(-3)-2xx(-12))=1/(1xx(-1)-2xx1)`
`⇒ x/(-3-12)=(-y)/(-3+24)=1/(-1-2)`
`⇒ x/-15=(-y)/21=1/-3`
`⇒ x/15=y/21=1/3`
`⇒ x=15/3,y =21/3`
`⇒ x=5,y=7`
Hence, the fraction is `5/7`
APPEARS IN
संबंधित प्रश्न
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
One says, "Give me a hundred, friend! I shall then become twice as rich as you". The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)
[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]
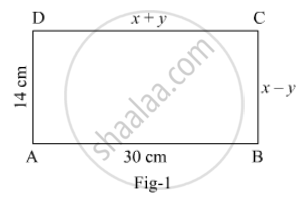
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Find the value of following determinant.
`|(-1,7),(2,4)|`
A and B each have a certain number of mangoes. A says to B, "if you give 30 of your mangoes, I will have twice as many as left with you." B replies, "if you give me 10, I will have thrice as many as left with you." How many mangoes does each have?
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find the number.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes `1/4`. Thus, we have
`(x-2)/(y+3)=1/4`
`⇒ 4(x-2)=y+3`
`⇒ 4x-8=y+3`
`⇒ 4x-y-11=0`
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes `2/3`. Thus, we have
`(x+6)/(3y)=2/3`
`⇒ 3(x+6)=6y`
`⇒ 3x +18 =6y`
`⇒ 3x-6y+18=0`
`⇒ 3(x-2y+6)=0`
`⇒ x-3y+6=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx6-(-2)xx(-11))=(-y)/(4xx6-1xx(-11))=1/(4xx(-2)-1xx(-1))`
`⇒ x/(-6-22)=-y/(24+11)=1/(-8+1)`
`⇒ x/-28=-y/35=1/-7`
`⇒ x= 28/7,y=35/7`
`⇒ x= 4,y=5`
Hence, the fraction is`4/5`
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B?
State with reason whether the point (3, −2) will lie on the graph of the equation 5m – 3n = − 21
