Advertisements
Advertisements
प्रश्न
A and B each have a certain number of mangoes. A says to B, "if you give 30 of your mangoes, I will have twice as many as left with you." B replies, "if you give me 10, I will have thrice as many as left with you." How many mangoes does each have?
उत्तर
To find:
(1) Total mangoes of A.
(2) Total mangoes of B.
Suppose A has x mangoes and B has y mangoes,
According to the given conditions,
`x + 30 =2(y - 30)`
`x+ 30 =2y -60`
`x - 2y +30 + 60 =0`
`x - 2y =90 =0`
`y +10 =3(x -10)`
`y +0 = 3x-30`
`y -3x +10+30 =0`
`y + 3x +40 =0`
`y - 3x +10 +30 =0`
`y - 3x +40 =0`
Multiplying eq. 1 by 3
3x + 6y + 270 = 0 …… (3) and
Now adding eq.2 and eq.3
5y = 310
`y = 310 /5`
`y = 62`
`x - 2xx62+90 =0`
`x - 124 + 90 =0`
`x - 34 = 0`
`x = 34`
Hence A has 34 mangoes and B has 62 mangoes.
APPEARS IN
संबंधित प्रश्न
Solve the following pairs of equations by reducing them to a pair of linear equations
6x + 3y = 6xy
2x + 4y = 5xy
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solve the following pair of linear equations.
152x − 378y = − 74
− 378x + 152y = − 604
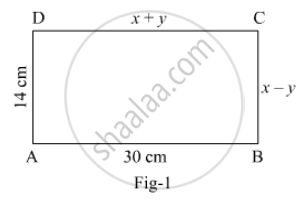
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator are increased by 3, they are in the ratio 2 : 3. Determine the fraction.
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B?
