Advertisements
Advertisements
प्रश्न
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
उत्तर
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
The numerator of the fraction is 4 less the denominator. Thus, we have
`x = y -4`
` ⇒ x -y =-4`
If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is 8 times the numerator. Thus, we have
` y + 1 = 8(x-2)`
`⇒ y + 1= 8x -16`
` ⇒ 8x -y = 1+16`
`⇒ 8x - y =17`
So, we have two equations
` x - y = -4`
` 8x -y =17`
Here x and y are unknowns. We have to solve the above equations for x and y.
Subtracting the second equation from the first equation, we get
`( x -y)-(8x -y)=-4-17`
`⇒ x - y -8x +y =-21`
` ⇒ -7 x =-21`
` ⇒ 7 x =21 `
` ⇒ x =21/7`
` ⇒ x = 3`
Substituting the value of x in the first equation, we have
` 3- y =-4`
`⇒ y = 3+4 `
` ⇒ y = 7`
Hence, the fraction is `3/7`
APPEARS IN
संबंधित प्रश्न
Solve `\frac{2}{x+2y}+\frac{6}{2x-y}=4\text{ ;}\frac{5}{2( x+2y)}+\frac{1}{3( 2x-y)}=1` where, x + 2y ≠ 0 and 2x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solve the following pair of linear equations
ax + by = c
bx + ay = 1 + c
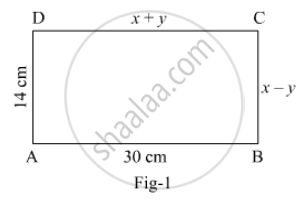
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
A and B each have a certain number of mangoes. A says to B, "if you give 30 of your mangoes, I will have twice as many as left with you." B replies, "if you give me 10, I will have thrice as many as left with you." How many mangoes does each have?
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes `1/4`. Thus, we have
`(x-2)/(y+3)=1/4`
`⇒ 4(x-2)=y+3`
`⇒ 4x-8=y+3`
`⇒ 4x-y-11=0`
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes `2/3`. Thus, we have
`(x+6)/(3y)=2/3`
`⇒ 3(x+6)=6y`
`⇒ 3x +18 =6y`
`⇒ 3x-6y+18=0`
`⇒ 3(x-2y+6)=0`
`⇒ x-3y+6=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx6-(-2)xx(-11))=(-y)/(4xx6-1xx(-11))=1/(4xx(-2)-1xx(-1))`
`⇒ x/(-6-22)=-y/(24+11)=1/(-8+1)`
`⇒ x/-28=-y/35=1/-7`
`⇒ x= 28/7,y=35/7`
`⇒ x= 4,y=5`
Hence, the fraction is`4/5`
A father is three times as old as his son. After twelve years, his age will be twice as that of his son then. Find the their present ages.
Two years ago, a father was five times as old as his son. Two year later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.
