Advertisements
Advertisements
प्रश्न
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Less than 19.5 hours?
उत्तर
Let x denotes the time taken to assemable cars mean µ = 20 hours and S.D σ = 2 hours
The standard normal variate
z = `(x - mu)/sigma`
= `(x - 20)/2`
P(less than 19.5 hours) = P(X < 19.5)
When x = 19.5
z = `19.5/2`
= `(-0.5)/2`
= 0.25
P(X < 19.5) = P(Z < – 0.25)
= P(`-oo` < z < 0) – P(– 0.25 < z < 0)
= 0.5 – P(0 < z < 0.25)
= 0.5 – 0.0987
= 0.4013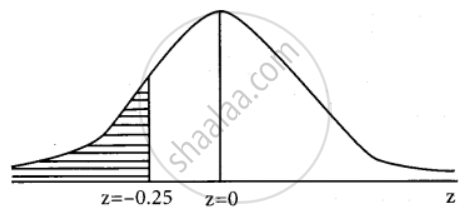
APPEARS IN
संबंधित प्रश्न
Define Bernoulli trials
Out of 750 families with 4 children each, how many families would be expected to have atmost 2 girls
The mean of a binomial distribution is 5 and standard deviation is 2. Determine the distribution
Derive the mean and variance of poisson distribution
Mention the properties of poisson distribution
In a test on 2,000 electric bulbs, it was found that bulbs of a particular make, was normally distributed with an average life of 2,040 hours and standard deviation of 60 hours. Estimate the number of bulbs likely to burn for more 1,920 hours but less than 2,100 hours
Choose the correct alternative:
If X ~ N(µ, σ2), the maximum probability at the point of inflexion of normal distribution
Choose the correct alternative:
Using the standard normal table, the sum of the probabilities to the right of z = 2.18 and to the left of z = – 1.75 is
Choose the correct alternative:
The time until the first failure of a brand of inkjet printers is normally distributed with a mean of 1,500 hours and a standard deviation of 200 hours. What proportion of printers fails before 1000 hours?
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Between 20 and 22 hours?
