Question

Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Raghul wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Raghul takes the test and scores 585. Will he be admitted to this university?

Answer 1

Let x denotes the scores of a national test mean

µ = 500 and standard deviation σ = 100

Standard normal variate z = `(x - mu)/sigma = (x - 5000)/100`

When x = 585

z = `(585 - 500)/100 = 85/100` = 0.85

P(X ≤ 585) = P(Z ≤ 0.85)

P(Z ≤ 0.85) = P(`-oo` < z < 0) + P(0 < z < 0.85)

= 0.5 + 0.3023

= 0.8023

For n = 100

P(Z ≤ 0.85) = 100 × 0.8023

= 80.23

∴ Raehul scores 80.23%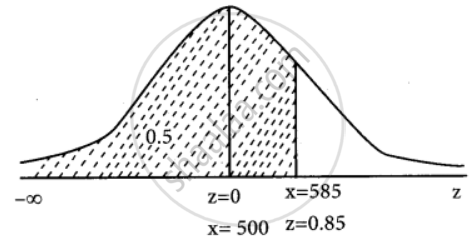

We can determine the scores of 70% of the students as follows:

From the table for the area 0.35

We get z₁ = – 1.4(as z₁ lies to left of z = 0)

Similarly z₂ = 1.4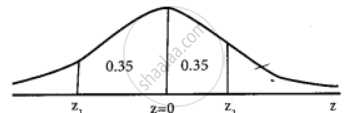

Now z₁ = `(x_1 - 500)/100`

⇒  – 1.4 = `(x_1 - 500)/100`

– 1.4 × 100 = x₁ – 500

⇒ x₁ 500 – 140

x₁ = 360

Again z₂ = `(x_2 - 500)/100`

⇒ – 1.4 = `(x_1 - 500)/100`

1.4 × 100 = x₂ – 500

⇒ x₂ = 140 + 500

= x₂ = 640

Hence 70% of students score between 360 and 640

But Raghul scored 585. His score is not better than the score of 70% of the students.

∴ He will not be admitted to the university.