Advertisements
Advertisements
प्रश्न
Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Raghul wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Raghul takes the test and scores 585. Will he be admitted to this university?
उत्तर
Let x denotes the scores of a national test mean
µ = 500 and standard deviation σ = 100
Standard normal variate z = `(x - mu)/sigma = (x - 5000)/100`
When x = 585
z = `(585 - 500)/100 = 85/100` = 0.85
P(X ≤ 585) = P(Z ≤ 0.85)
P(Z ≤ 0.85) = P(`-oo` < z < 0) + P(0 < z < 0.85)
= 0.5 + 0.3023
= 0.8023
For n = 100
P(Z ≤ 0.85) = 100 × 0.8023
= 80.23
∴ Raehul scores 80.23%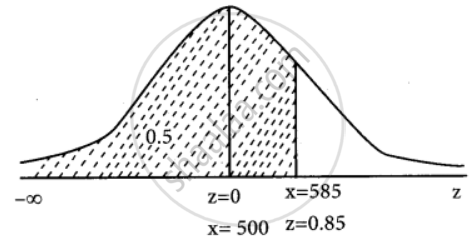
We can determine the scores of 70% of the students as follows:
From the table for the area 0.35
We get z1 = – 1.4(as z1 lies to left of z = 0)
Similarly z2 = 1.4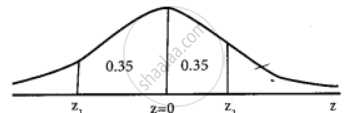
Now z1 = `(x_1 - 500)/100`
⇒ – 1.4 = `(x_1 - 500)/100`
– 1.4 × 100 = x1 – 500
⇒ x1 500 – 140
x1 = 360
Again z2 = `(x_2 - 500)/100`
⇒ – 1.4 = `(x_1 - 500)/100`
1.4 × 100 = x2 – 500
⇒ x2 = 140 + 500
= x2 = 640
Hence 70% of students score between 360 and 640
But Raghul scored 585. His score is not better than the score of 70% of the students.
∴ He will not be admitted to the university.
APPEARS IN
संबंधित प्रश्न
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers, what is the probability that 12 of the travelers will not have a laptop?
Consider five mice from the same litter, all suffering from Vitamin A deficiency. They are fed a certain dose of carrots. The positive reaction means recovery from the disease. Assume that the probability of recovery is 0.73. What is the probability that atleast 3 of the 5 mice recover
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be no phone at all
In a photographic process, the developing time of prints may be looked upon as a random variable having the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second. Find the probability that it will take less than 16.35 seconds to develop prints
Time taken by a construction company to construct a flyover is a normal variate with mean 400 labour days and a standard deviation of 100 labour days. If the company promises to construct the flyover in 450 days or less and agree to pay a penalty of ₹ 10,000 for each labour day spent in excess of 450. What is the probability that the company takes at most 500 days to complete the flyover?
Choose the correct alternative:
If X ~ N(µ, σ2), the maximum probability at the point of inflexion of normal distribution
Choose the correct alternative:
In turning out certain toys in a manufacturing company, the average number of defectives is 1%. The probability that the sample of 100 toys there will be 3 defectives is
Choose the correct alternative:
Using the standard normal table, the sum of the probabilities to the right of z = 2.18 and to the left of z = – 1.75 is
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X < 40)
People’s monthly electric bills in Chennai are normally distributed with a mean of ₹ 225 and a standard deviation of ₹ 55. Those people spend a lot of time online. In a group of 500 customers, how many would we expect to have a bill that is ₹ 100 or less?
