Advertisements
Advertisements
प्रश्न
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
उत्तर
(i) F = `Q_q/r^2` = 1 dyne = `([1 "esu of charge"]^2)/[1 cm]^2`
Or, 1 esu of charge = 1 (dyne)1/2 (cm)
Hence, [1 esu of charge] = [F]1/2 L = [MLT–2]1/2 L = M1/2 L3/2 T–1
[1 esu of charge] = M1/2 L3/2 T–1
Thus charge in cgs unit is expressed as fractional powers (1/2) of M and (3/2) of L.
(ii) Consider the coloumb force on two charges, each of magnitude 1 esu of charge separated by a distance of 1 cm:
The force is then 1 dyne = 10–5N.
This situation is equivalent to two charges of magnitude x C separated by 10–2m.
This gives: F = `1/(4piε_0) * x^2/10^-4` which should be 1 dyne = 10–5 N.
Thus `1/(4 piε_0) * x^2/10^-4 = 10^-5` ⇒ `1/(4 piε_0) = 10^-9/x^2 (Nm^2)/C^2`
With `x = 1/([3] xx 10^9)`, this yields
`1/(4 piε_0) = 10^-9 xx [3]^2 xx 10^18 = [3]^2 xx 10^9 (Nm)^2/C^2`
With [3] → 2.99792458, we get
`1/(4 piε_0) = 8.98755.... xx 10^9 (Nm^2)/C^2` exactly
APPEARS IN
संबंधित प्रश्न
Suppose that the particle is an electron projected with velocity vx = 2.0 × 106 m s−1. If E between the plates separated by 0.5 cm is 9.1 × 102 N/C, where will the electron strike the upper plate? (|e| = 1.6 × 10−19 C, me = 9.1 × 10−31 kg)
Two equal charges are placed at a separation of 1.0 m. What should be the magnitude of the charges, so that the force between them equals the weight of a 50 kg person?
Find the ratio of the electrical and gravitational forces between two protons.
How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?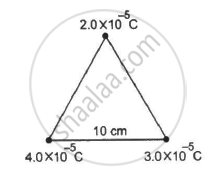
Write a short note on superposition principle.
Two point charges +3 µC and +8 µC repel each other with a force of 40 N. If a charge of -5 µC is added to each of them, then force between them will become ______.
For charges q1 and q2 separated by a distance R the magnitude of the electrostatic force is given by ______.
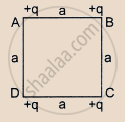
Four equal charges q are placed at the four comers A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be ______.
Two charge – 10c and + 10 c are placed 10 cm apart. Potential at centre of the line joining the two charge is:-
Two point charges +2 C and +6 C repel each other with a force of 12 N. If a charge of -4 C is given to each of these charges, then the force now is ______.
