Advertisements
Advertisements
प्रश्न
Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet distance from the wall to which the gate is fixed. If one of the gates is opened to 90°, find the distance moved by the wheel (π = 3.14)
उत्तर
Let A be the position of the wall AC be the gate in initial position and AB be position when it is moved 90°.
Now the arc length BC gives the distance moved by the wheel.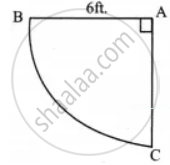
Length of the arc = `theta^circ/(360^circ) xx 2pi"r units"`
= `(90^circ)/(360^circ) xx 2 xx 3.14 xx 6 "feet"`
= 3.14 × 3 feet
= 9.42 feet
∴ Distance moved by the wheel = 9.42 feet.
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 10 cm. The measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (\[\pi\]= 3.14 )
Area of a sector of a circle of radius 15 cm is 30 cm2 . Find the length of the arc of the sector.
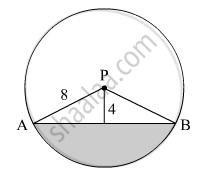
In the given figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion. ( \[\pi\] = 3.14, \[\sqrt{3}\]= 1.73 )

In the given figure, square ABCD is inscribed in the sector A - PCQ. The radius of sector C - BXD is 20 cm. Complete the following activity to find the area of shaded region
In Δ ABC, if ∠ A = 65° ; ∠ B = 40° then find the measure of ∠ C.
Measure of an arc of a sector of a circle is 900 and its radius is 7cm. Find the perimeter of the sector.
(A) 44 cm (B) 25 cm (C) 36 cm (D) 56 cm
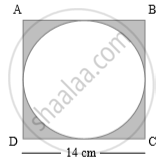
A circle is inscribed in square ABCD of side 14 cm. Complete the following activity to find the area of the shaded portion.
Activity:
Area of square ABCD = ______
= 142
= 196 cm2
Area of circle = πr2 = `22/7xx 7^2`
= ____ cm2
Area of shaded portion = Area of square ABCD – Area of circle
= 196 – _______
= _____ cm2
Match the following:
| Column A | Column B |
| (i) Area of a circle | (a) `1/4 pi"r"^2` |
| (ii) Circumference of a circle | (b) (π + 2)r |
| (iii) Area of the sector of a circle | (c) πr2 |
| (iv) Circumference of a semicircle | (d) 2πr |
| (v) Area of a quadrant of a circle | (e) `theta^circ/360^circ xx pi"r"^2` |
A circle of radius 120 m is divided into 8 equal sectors. Find the length of the arc of each of the sectors
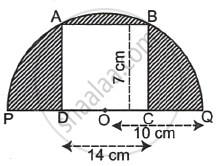
In the given figure, a rectangle ABCD is inscribed inside a semi-circle of radius 10 cm. Using the dimensions given in the figure, determine the area of the shaded region.