Advertisements
Advertisements
प्रश्न
Two metallic wires, P1 and P2 of the same material and same length but different cross-sectional areas, A1 and A2 are joined together and connected to a source of emf. Find the ratio of the drift velocities of free electrons in the two wires when they are connected (i) in series, and (ii) in parallel.
उत्तर
\[\text { Drift velocity of free electrons is given by }: \]
\[ v_d = \frac{I}{Ane}\]
\[or, v_d \propto \frac{I}{A}\]
\[\text { where A is the area of the conductor and I is the current flowing through the conductor } . \]
\[(i) \text { When the two conductors are connected in series, the current is same through the two wires }\]
\[\text { Therefore, required ratio of drift velocity of free electrons in wire } P_1 to P_2 is\]
\[\frac{v_{d_{P_1}}}{v_{d_{P_2}}} = \frac{I \times A_2}{I \times A_1} = A_2 : A_1 \]
\[\text { where, v_{d_{P_1}} is the drift velocity of electrons in wire} P_1 \text { and } v_{d_{P_2}} \text { is the drift velocity of electrons in wire } P_2 \]
\[(ii) \text { When the two conductors are connected in parallel, the potential drop aross both the conductor is same } . \]
\[ \Rightarrow v_{d_{P_1}} = \frac{V}{R_1 A_1} = \frac{V}{\frac{\rho l}{A_1} A_1} = \frac{V}{\rho l} \text { and } v_{d_{P_2}} = \frac{V}{R_2 A_2} = \frac{V}{\frac{\rho l}{A_2} A_2} = \frac{V}{\rho l}\]
\[\text { Therefore, required ratio of drift velocity of free electrons in wire } P_1 to P_2 is\]
\[\frac{v_{d_{P_1}}}{v_{d_{P_2}}} = \frac{\frac{V}{\rho l}}{\frac{V}{\rho l}} = 1: 1\]
APPEARS IN
संबंधित प्रश्न
A wheel with 8 metallic spokes each 50 cm long is rotated with a speed of 120 rev/min in a plane normal to the horizontal component of the Earth’s magnetic field. The Earth’s magnetic field at the place is 0.4 G and the angle of dip is 60°. Calculate the emf induced between the axle and the rim of the wheel. How will the value of emf be affected if the number of spokes were increased?
Answer the following question.
Two bulbs are rated (P1, V) and (P2, V). If they are connected (i) in series and (ii) in parallel across a supply V, find the power dissipated in the two combinations in terms of P1 and P2.
100 cells each of emf 5 V and internal resistance 1 Ω are to be arranged so as to produce maximum current in a 25 Ω resistance. Each row contains equal number of cells. The number of rows should be ______.
Choose the correct alternative.
Five dry cells each of voltage 1.5 V are connected as shown in the diagram

What is the overall voltage with this arrangement?
Give reason/short answer.
In the given circuit diagram two resistors are connected to a 5V supply.

A third resistor is now connected in parallel with 6Ω resistor. Will the potential difference across the 8Ω resistor the larger, smaller, or the same as before? Explain the reason for your answer.
Two metal wires of identical dimensions are connected in parallel. If σ1 and σ2 are the conductivities of the metal wires respectively, the effective conductivity of the combination is
When cells are connected in parallel, then ______
Two cells of emf’s approximately 5V and 10V are to be accurately compared using a potentiometer of length 400 cm.
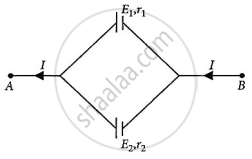
Two cells of emfs E1 and E2 and internal resistances r1 and r2 respectively are connected in parallel as shown in the figure. Deduce the expression for the
- equivalent emf of the combination
- equivalent internal resistance of the combination
- potential difference between the points A and B.
The equivalent resistance of series combination of two resistors is 's'. When they are connected in parallel, the equivalent resistance is 'p'. If s = np, then the minimum value for n is ______. (Round off to the Nearest Integer)
