Advertisements
Advertisements
प्रश्न
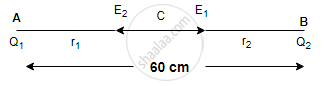
Two-point charges Q1 = 400 μC and Q2 = 100 μC are kept fixed, 60 cm apart in a vacuum. Find the intensity of the electric field at the midpoint of the line joining Q1 and Q2.
उत्तर
`"E"_1 = "Q"_1/(4 piin_0 "r"_1^2)` ... `["Q"_1 = 400mu"C" = 400 xx 10^-6"C"]`
`"E"_2 = "Q"_2/(4 piin_0 "r"_2^2)` ...`["Q"_2 = 100mu"C" = 100 xx 10^-6"C"]`
∴ The resultant electric field
E = E2 - E1
`= "Q"_2/(4 piin_0 "r"_2^2) - "Q"_1/(4 piin_0 "r"_1^2)`
`= 1/(4 piin_0 "r"^2) ... ["Q"_2 - "Q"_1][because "r"_1 = "r"_2 = "r"]`
`=(9 xx 10^9)/(30/100)^2 [400 - 100]xx10^-6`
`= (9xx10^11xx10^-6[3]xx100)/9`
`= 3 xx 10^7 "NC"^-1`
From Q1 to Q2
APPEARS IN
संबंधित प्रश्न
A system has two charges qA = 2.5 × 10−7 C and qB = −2.5 × 10−7 C located at points A: (0, 0, − 15 cm) and B: (0, 0, + 15 cm), respectively. What are the total charge and electric dipole moment of the system?
An electric dipole is placed at the centre of a sphere. Mark the correct options.
(a) The flux of the electric field through the sphere is zero.
(b) The electric field is zero at every point of the sphere.
(c) The electric field is not zero anywhere on the sphere.
(d) The electric field is zero on a circle on the sphere.
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the axis of the dipole 1.0 cm away from the centre.
Two particles A and B, of opposite charges 2.0 × 10−6 C and −2.0 × 10−6 C, are placed at a separation of 1.0 cm. Calculate the electric field at a point on the perpendicular bisector of the dipole and 1.0 m away from the centre.
An electric dipole consists of two opposite charges each 0.05 µC separated by 30 mm. The dipole is placed in an unifom1 external electric field of 106 NC-1. The maximum torque exerted by the field on the dipole is ______
Two charges + 3.2 x 10-19 C and --3.2 x 10-19 C placed at 2.4 Å apart to form an electric dipole. lt is placed in a uniform electric field of intensity 4 x 105 volt/m. The electric dipole moment is ______.
On the axis and on the equator of an electric dipole for all points ____________.
What work must be done to rotate an electric dipole through an angle θ with the electric field, if an electric dipole of moment p is placed in a uniform electric field E with p parallel to E?
Show that intensity of electric field at a point in broadside position of an electric dipole is given by:
E = `(1/(4piepsilon_0)) "p"/(("r"^2 + l^2)^(3//2))`
Where the terms have their usual meaning.
