Question

Two straight paths are represented by the linear equations 2x – 4y = 4 and – 6x + 12y = 6. Check whether the paths cross each other or not, by using the graphical representation.

Answer 1

The given equations are as follows:

2x – 4y = 4   ......(i)

And – 6x + 12y = 6   ......(ii)

From equation (i), we have

y = `(2x - 4)/4`

For x = 0, y = `(2(0) - 4)/4 = (-4)/4` = – 1

For x = 2, y = `(2(2) - 4)/4 = (4 - 4)/4` = 0

x	0	2
y	– 1	0
(x, y)	(0, – 1)	(2, 0)

From equation (ii), we have

y = `(6 + 6x)/12`

For x = 0, y = `(6 + 6(0))/12 = 6/12 = 1/2` = 0.5

For x = – 1, y = `(6 + 6(-1))/12 = (6 - 6)/2` = 0

x	0	– 1
y	0.5	0
(x, y)	(0, 0.5)	(– 1, 0)

The graphical representation is as follows: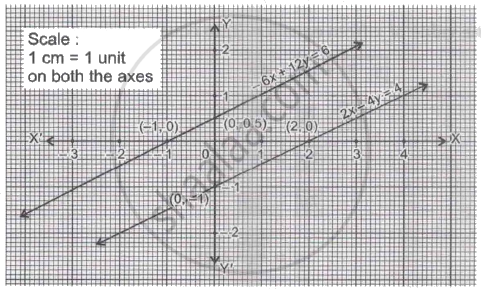

The two straight routes do not intersect one other, as shown in the graph above. As a result, there is no common solution to the presented equations.