Advertisements
Advertisements
प्रश्न
Using Biot Savarts law, obtain the expression for the magnetic induction near a straight infinitely long current-carrying wire.
उत्तर
- Consider a straight wire of length l carrying current I.
- Let a point P situated at a perpendicular distance R from the wire as shown below.
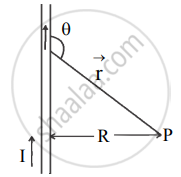
- Consider infinitesimal length `vec"d"`l of wire carrying current I, then-current element = `"I"vec"d"l` .
- The current element is situated at distance r from point P making an angle θ, as shown in the figure above.
- Using Biot Savart law, magnetic field, produced `vec"dB"` at P due to current element `"I"vec"d"l` is,
`vec"dB" = mu_0/(4pi) ("I"vec"d"l sin theta)/"r"^2` ....(1) - According to properties of cross-product, `vec"d"l xx vec"r"` indicates the direction of `vec"dB"`, in this case, is into the plane of the paper.
- Summing up all current elements from the upper half of infinitely long wire,
Bupper = `int_0^∞ "dB" = mu_0/(4pi) int_0^∞ ("I"vec"d"l sintheta)/"r"^2` ….(2) - Taking into account the symmetry of wire, current elements in the lower half of infinitely long wire will also contribute the same as the upper half.
i.e., `"B"_"lower" = "B"_"upper"` ….(3) - Adding contributions from the lower and upper part, total magnetic field point P is
B = `2int_0^∞ "dB"` ….[using equation (2)]
= `(2mu_0)/(4pi) int_0^∞ ("Id"l sintheta)/"r"^2` ….[using equation (1)]
But r = `sqrt(l^2 + "R"^2)` and
sin θ = sin (π - θ)
= `"R"/"r"`
= `"R"/sqrt(l^2 + "R"^2)`
∴ B = `(mu_0"I")/(2pi) int_0^∞ ("Rdl")/((l^2 + "R"^2)sqrt(l^2 + "R"^2))`
= `(mu_0"I")/(2pi) "R" int_0^∞ "dl"/(l^2 + "R"^2)^{3/2}`
Solving the integration,
B = `(mu_0"I")/(2pi) "R" xx 1/"R"^2 = (mu_0"I")/(2pi"R")` ….(4)
This is the equation for magnetic field at a point situated at a perpendicular distance R from infinitely long wire carrying current I.
APPEARS IN
संबंधित प्रश्न
Explain Biot Savart's Law.
Which of the following graphs shows the variation of magnetic field B, with distance for a long current carrying conductor?
A long straight wire carries a current of π ampere. The magnetic field due to it will be 10 x `10^-5` weber/m2 at what distance from the wire
[µ0 = permeability of air]?
The value of magnetic induction will be minimum at a point due to a small current carrying conductor when angle between element and line joining point and centre of element is ____________.
The magnetic induction at a point P which is at a distance of 2 cm from a long current-carrying wire is 10-6 T. The induction at a distance 8 cm from same current-carrying wire is ______.
The magnetic field at the centre of coil of n turns, bent in the form of a square of side `2l`, carrying current i, is ____________.
A current 'I' is flowing along an infinite, straight wire, in the positive Z-direction and the same current is flowing along a similar parallel wire 5 m apart, in the negative Z-direction. A point P is at a perpendicular distance 3 m from the first wire and 4 m from the second. What will be magnitude of the magnetic field B at P?
A straight wire carrying current 'I' is bent into a semi-circular arc of radius 'r', as shown. The magnitude of magnetic field at point 'O' due to semi-circular arc is (µ0 = Permeability of free space) ____________.

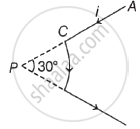
A current path shaped as shown in figure produces a magnetic field at P, the centre of the arc. If the arc subtends an angle of 30° and the radius of arc is 0.6 m. What is the magnitude of the field at P, if the current is 3.0 A?
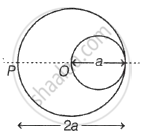
A cylindrical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given `"N"/12`µ0aJ, then the value of N is ______.