Advertisements
Advertisements
प्रश्न
Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
उत्तर
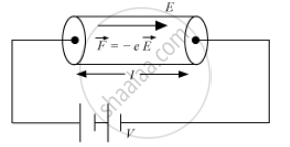
The drift velocity of electrons in a conductor is given as
V_d = `(eEr)/m` ...(1)
where,
E = electric field set up across a conductor
m = mass of the electron
τ" data-mce-style="display: inline; font-style: normal; font-weight: 400; line-height: normal; font-size: 16px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: 0px; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; color: #212121; font-family: Roboto, sans-serif; font-variant-ligatures: normal; font-variant-caps: normal; orphans: 2; widows: 2; -webkit-text-stroke-width: 0px; background-color: #ffffff; text-decoration-style: initial; text-decoration-color: initial; position: relative;" data-mce-tabindex="0">ττ = average relaxation time
Now the current flowing in the conductor can be derived as
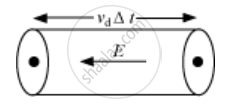
Electron drift to a small distance in a time Δt = VdΔt
Amount of charge passing through the area A in time Δt, q = IΔt
IΔt = neAvdΔt
or I = neAvd ...(2)
Where,
n → Number of free electrons per unit volume or number density.
Now from equation (1) and (2), we get
`I = ("ne"^2ArE)/m` ....3
Since the resistivity of a conductor is given as
`rho = m/("ne"^2r)`
Now, we know that conductivity of a conductor is mathematically defined as the reciprocal of resistivity of the conductor. Thus
`rho = 1/sigma` ....(4)
where `sigma = `conductivity of the conductor. Thus, from equation (3) and (4), we get
`sigma = ("ne"^2r)/m` ...(5)
Now, from equation (3) and (5), we have
`I/A = sigmaE .....(6)`
and the current density is given as
`J = I/A`
Thus `J =sigmaE`
APPEARS IN
संबंधित प्रश्न
Define current density. Write an expression which connects current density with drift speed
The heat developed in a system is proportional to the current through it.
An electrolysis experiment is stopped and the battery terminals are reversed.
The specification on a heater coil is 250 V, 500 W. Calculate the resistance of the coil. What will be the resistance of a coil of 1000 W to operate at the same voltage?
What is the colour code of a carbon resistor having a resistance of 470 Ω and a tolerance of 5%?
Two cells of 1.25 V and 0.75 V are connected in series with anode of one connected to cathode of the other. The effective voltage will be ______.
A constant voltage is applied between the two ends of a uniform metallic wire, heat ‘H’ is developed in it. If another wire of the same material, double the radius and twice the length as compared to the original wire is used then the heat developed in it will be -
The resistivity of a wire ______
