Advertisements
Advertisements
Question
Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
Solution
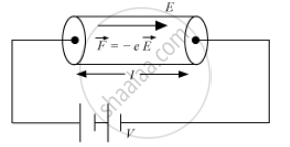
The drift velocity of electrons in a conductor is given as
V_d = `(eEr)/m` ...(1)
where,
E = electric field set up across a conductor
m = mass of the electron
τ" data-mce-style="display: inline; font-style: normal; font-weight: 400; line-height: normal; font-size: 16px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: 0px; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; color: #212121; font-family: Roboto, sans-serif; font-variant-ligatures: normal; font-variant-caps: normal; orphans: 2; widows: 2; -webkit-text-stroke-width: 0px; background-color: #ffffff; text-decoration-style: initial; text-decoration-color: initial; position: relative;" data-mce-tabindex="0">ττ = average relaxation time
Now the current flowing in the conductor can be derived as
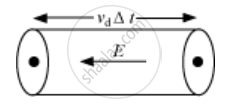
Electron drift to a small distance in a time Δt = VdΔt
Amount of charge passing through the area A in time Δt, q = IΔt
IΔt = neAvdΔt
or I = neAvd ...(2)
Where,
n → Number of free electrons per unit volume or number density.
Now from equation (1) and (2), we get
`I = ("ne"^2ArE)/m` ....3
Since the resistivity of a conductor is given as
`rho = m/("ne"^2r)`
Now, we know that conductivity of a conductor is mathematically defined as the reciprocal of resistivity of the conductor. Thus
`rho = 1/sigma` ....(4)
where `sigma = `conductivity of the conductor. Thus, from equation (3) and (4), we get
`sigma = ("ne"^2r)/m` ...(5)
Now, from equation (3) and (5), we have
`I/A = sigmaE .....(6)`
and the current density is given as
`J = I/A`
Thus `J =sigmaE`
APPEARS IN
RELATED QUESTIONS
The following figure shows a conductor of length l with a circular cross-section. The radius of the cross-section varies linearly from a to b. The resistivity of the material is ρ. Assuming that b – a << l, find the resistance of the conductor.

For a metallic conductor, what is the relation between current density (J), conductivity (σ) and electric field intensity (E)?
What is the colour code of a carbon resistor having a resistance of 470 Ω and a tolerance of 5%?
Consider a current carrying wire (current I) in the shape of a circle.
Assertion: Bending a wire does not effect electrical resistance.
Reason: Resistance of wire is proportional to resistivity of material.
The equivalent resistance between A and B is ____________.
A man covers his body with a blanket of thickness 4 mm. His temperature is 37°C and that of the atmosphere is 27°C. If the coefficient of thermal conductivity of wool is 1.2 × 10-5 MKS units, heat lost by him per hour per square meter area is:
As the temperature of conductor increase, it's resistivity and conductivity change. The ratio of resistivity to conductivity.
The resistivity of a wire ______
