Advertisements
Advertisements
प्रश्न
Using the geometry of the double slit experiment, derive the expression for fringe width of interference bands.
उत्तर
Let S1 and S2 be the two sources of light separated by distance d. A screen is placed at a distance of D from the two light sources. Let 'A be the wavelength of light.
Draw S1 S'1 and S2 S'2 perpendicular to the screen. Let O' be the midpoint of S'1 S'2.
∴ `O"'"S"'"_1 = O"'"S"'"_1 = d/2`
Let 'P' be the point at distance y from point 'O' on screen.
Finding whether point P is bright or dark depends upon the path difference. The path difference is S2P − S1P.
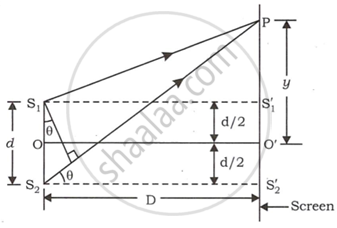
In ΔS1S'1P,
(S1P)2 = (S1S'1)2 + (S'1P)2
`(S_1P)^2 = D^2 + (y - d/2)^2`
`(S_1P)^2 = D^2 + y^2 - yd + d^2/4` ...(i)
In ΔS2S'2P,
(S2P)2 = (S2S'2)2 + (S'2P)2
`(S_2P)^2 = D^2 + (y + d/2)^2`
`(S_2P)^2 = D^2 + y^2 + yd + d^2/4` ...(ii)
Subtracting equation (i) from (ii),
(S2P)2 − (S1P)2
= `(D^2 + y^2 + yd + d^2/4) - (D^2 + y^2 - yd + d^2/4)`
∴ (S2P + S1P)(S2P − S1P) = 2yd
We know (S2P − S1P) = Path difference
∴ Path difference = `(2yd)/((S_P + S_1P))`
Now, D is very large as compared to y and
i.e. D >> y and D >> d.
∴ S2P ≈ S1P ≈ D
∴ Path difference = `(2yd)/(D + D) = (2yd)/(2D)`
∴ Path difference = `(yd)/D` ...(iii)
Case-I:
The point P will be bright if the path difference = nλ
`therefore (yd)/D = n lambda`
`y = (D n lambda)/d`
Equation for position of nth bright band is
`therefore y_n = (D n lambda)/d` ...(iv)
Case-II:
The point P will be dark if path difference = `(2n - 1)lambda/2`
`therefore (yd)/D = (2n - 1)lambda/2`
`therefore y = (D(2n - 1)lambda)/(2 d)`
The equation for position of the nth dark band is
`therefore y_n = (D(2n - 1)lambda)/(2d)` ...(v)
Fringe width (W): The distance between two successive bright or dark bands in an interference pattern is called fringe width or bandwidth.
∴ Fringe width (W) = yn + 1 − yn
From equation (iv),
Equation of nth bright band
`y_n = (D n lambda)/d`
The equation for (n + 1)th bright band
`y_(n + 1) = (D(n + 1)lambda)/d`
∴ Fringe width (W) = yn + 1 − yn
= `(D(n + 1)lambda)/d - (D n lambda)/d`
= `(D lambda)/d [(n + 1) - n]`
= `(D lambda)/d(1)`
∴ Fringe width (W) = `(lambda D)/d`
APPEARS IN
संबंधित प्रश्न
What is the diffraction of light? How does it differ from interference? What are Fraunhofer and Fresnel diffractions?
In a biprism experiment, the fringes are observed in the focal plane of the eyepiece at a distance of 1.2 m from the slits. The distance between the central bright and the 20th bright band is 0.4 cm. When a convex lens is placed between the biprism and the eyepiece, 90 cm from the eyepiece, the distance between the two virtual magnified images is found to be 0.9 cm. Determine the wavelength of light used.
What must be the ratio of the slit width to the wavelength of light for a single slit to have the first diffraction minimum at 45.0°?
What should be the slit width to obtain pronounced diffraction with a single slit illuminated by the light of wavelength λ?
What is the difference between Fresnel and Fraunhofer diffraction?
A lens having focal length f gives Fraunhofer type diffraction pattern of a slit having width a. If wavelength of light is λ, the distance of first dark band and next bright band from axis is given by ____________.
Light of wavelength 'λ' is incident on a single slit of width 'a' and the distance between slit and screen is 'D'. In diffraction pattern, if slit width is equal to the width of the central maximum then 'D' is equal to ______.
In a single slit diffraction experiment. fir t minimum for red light (589 nm) coincides with first maximum of some other wavelength `lambda'`. The value of `lambda'` is ______.
In a diffraction pattern, width of a fringe ____________.
The angular spread of central maximum, in diffraction pattern, does not depend on ______.
The diffraction fringes obtained by a single slit are of ____________.
Select the CORRECT statement from the following.
The first minimum of a single slit diffraction pattern is observed at angle 2° with a light of wavelength 510 nm. The width of this slit is ____________.
A plane wavefront of wavelength `lambda`. is incident on a slit of width a. The angular width of principal maximum is ______.
When two coherent sources in Young's experiment are far apart, then interference pattern ______
A physical quantity P is described by the relation p = a1/2 b2 c3 d-4. If the relative errors in the measurement of a, b, c and d respectively, are 2%, 1%, 3% and 5%, then the relative error in P will be ______.
In a Young's double-slit experiment, let β be the fringe width, and let I0 be the intensity at the central bright fringe. At a distance x from the central bright fringe, the intensity will be ______.
The fringe width in a Young's double slit experiment can be increased if we decrease ______.
In Fraunhoffer diffraction experiment, L is the distance between the screen and the obstacle, b is the size of the obstacle and λ is the wavelength of the incident light. The general condition for the applicability of Fraunhoffer diffraction is ______.
A mixture of light, consisting of wavelength 590 nm and an unknown wavelength, illuminates Young's double slit and gives rise to two overlapping intererence patterns on the screen. The central maximum of both lights coincides.
Further, it is observed that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data the wavelength of the unknown light is ______.
In a Young’s experiment, two coherent sources are placed 0.90 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1mm from the central fringe, then the wavelength of monochromatic light used will be ______.
In Young's double slit experiment, the 8th maximum with wavelength λ1 is at a distance d1 from the central maximum and the 6th maximum with a wavelength λ2 is at a distance d2. Then d1/d2 is equal to ______.
In a Young's double slit experiment carried out with light of wavelength λ = 5000 Å, the distance between the slits is 0.2 mm and the screen is at 200 cm from the slits. The central maximum is at x = 0. The third maximum (taking the central maximum as zeroth maximum) will be at x equal to ______.
Two coherent monochromatic light beams of amplitudes E10 and E20 produce an interference pattern. The ratio of the intensities of the maxim a and minima in the interference pattern is ______.
