Advertisements
Advertisements
Question
Using the geometry of the double slit experiment, derive the expression for fringe width of interference bands.
Solution
Let S1 and S2 be the two sources of light separated by distance d. A screen is placed at a distance of D from the two light sources. Let 'A be the wavelength of light.
Draw S1 S'1 and S2 S'2 perpendicular to the screen. Let O' be the midpoint of S'1 S'2.
∴ `O"'"S"'"_1 = O"'"S"'"_1 = d/2`
Let 'P' be the point at distance y from point 'O' on screen.
Finding whether point P is bright or dark depends upon the path difference. The path difference is S2P − S1P.
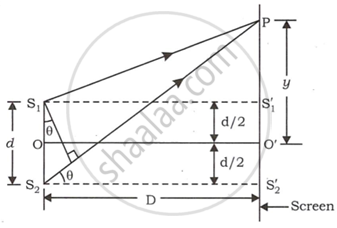
In ΔS1S'1P,
(S1P)2 = (S1S'1)2 + (S'1P)2
`(S_1P)^2 = D^2 + (y - d/2)^2`
`(S_1P)^2 = D^2 + y^2 - yd + d^2/4` ...(i)
In ΔS2S'2P,
(S2P)2 = (S2S'2)2 + (S'2P)2
`(S_2P)^2 = D^2 + (y + d/2)^2`
`(S_2P)^2 = D^2 + y^2 + yd + d^2/4` ...(ii)
Subtracting equation (i) from (ii),
(S2P)2 − (S1P)2
= `(D^2 + y^2 + yd + d^2/4) - (D^2 + y^2 - yd + d^2/4)`
∴ (S2P + S1P)(S2P − S1P) = 2yd
We know (S2P − S1P) = Path difference
∴ Path difference = `(2yd)/((S_P + S_1P))`
Now, D is very large as compared to y and
i.e. D >> y and D >> d.
∴ S2P ≈ S1P ≈ D
∴ Path difference = `(2yd)/(D + D) = (2yd)/(2D)`
∴ Path difference = `(yd)/D` ...(iii)
Case-I:
The point P will be bright if the path difference = nλ
`therefore (yd)/D = n lambda`
`y = (D n lambda)/d`
Equation for position of nth bright band is
`therefore y_n = (D n lambda)/d` ...(iv)
Case-II:
The point P will be dark if path difference = `(2n - 1)lambda/2`
`therefore (yd)/D = (2n - 1)lambda/2`
`therefore y = (D(2n - 1)lambda)/(2 d)`
The equation for position of the nth dark band is
`therefore y_n = (D(2n - 1)lambda)/(2d)` ...(v)
Fringe width (W): The distance between two successive bright or dark bands in an interference pattern is called fringe width or bandwidth.
∴ Fringe width (W) = yn + 1 − yn
From equation (iv),
Equation of nth bright band
`y_n = (D n lambda)/d`
The equation for (n + 1)th bright band
`y_(n + 1) = (D(n + 1)lambda)/d`
∴ Fringe width (W) = yn + 1 − yn
= `(D(n + 1)lambda)/d - (D n lambda)/d`
= `(D lambda)/d [(n + 1) - n]`
= `(D lambda)/d(1)`
∴ Fringe width (W) = `(lambda D)/d`
APPEARS IN
RELATED QUESTIONS
In Fraunhoffer diffraction by a narrow slit, a screen is placed at a distance of 2 m from the lens to obtain the diffraction pattern. If the slit width is 0.2 mm and the first minimum is 5 mm on either side of the central maximum, find the wavelength of light.
What is the diffraction of light? How does it differ from interference? What are Fraunhofer and Fresnel diffractions?
The bending of a beam of light around corners of obstacle is called ______
What should be the slit width to obtain pronounced diffraction with a single slit illuminated by the light of wavelength λ?
What must be the ratio of the slit width to the wavelength for a single slit, to have the first diffraction minimum at 45˚?
In biprism experiment, the distance between source and eyepiece is 1.2 m, the distance between two virtual sources is 0.84 mm. Then the wavelength of light used if eyepiece is to be moved transversely through a distance of 2.799 cm to shift 30 fringes is ______.
A lens having focal length f gives Fraunhofer type diffraction pattern of a slit having width a. If wavelength of light is λ, the distance of first dark band and next bright band from axis is given by ____________.
The luminous border that surrounds the profile of a mountain just before sun rises behind it, is an example of ______.
In a diffraction pattern, width of a fringe ____________.
The angular spread of central maximum, in diffraction pattern, does not depend on ______.
The condition for observing Fraunhofer diffraction pattern from an obstacle is that the light wavefront incident on it must be ______.
The first minimum of a single slit diffraction pattern is observed at angle 2° with a light of wavelength 510 nm. The width of this slit is ____________.
A parallel beam of monochromatic light falls normally on a single narrow slit. The angular width of the central maximum in the resulting diffraction pattern ______
A plane wavefront of wavelength `lambda`. is incident on a slit of width a. The angular width of principal maximum is ______.
In Fraunhofer diffraction due to single slit, the angular width of central maximum does 'NOT' depend on ______
A parallel beam of monochromatic light of wavelength 5 × 10-7 m is incident normally on a single narrow slit of width 10-3 mm. At what angle of diffraction, the first minima are observed?
In young 's double slit experiment the two coherent sources have different amplitudes. If the ratio of maximum intensity to minimum intensity is 16 : 1, then the ratio of amplitudes of the two source will be _______.
In Young's double slit experiment, the fringe width is 12 mm. If the entire arrangement is placed in water of refractive index `4/3`, then the fringe width becomes (in mm) ______.
The fringe width in a Young's double slit experiment can be increased if we decrease ______.
The increase in energy of a metal bar of length 'L' and cross-sectional area 'A' when compressed with a load 'M' along its length is ______.
(Y = Young's modulus of the material of metal bar)
In Fraunhofer diffraction pattern, slit width is 0.2 mm and screen is at 2 m away from the lens. If wavelength of light used is 5000 Å, then the distance between the first minimum on either side of the central maximum is ______. (θ is small and measured in radian)
In Young's double slit experiment, the 8th maximum with wavelength λ1 is at a distance d1 from the central maximum and the 6th maximum with a wavelength λ2 is at a distance d2. Then d1/d2 is equal to ______.
In a Young's double slit experiment carried out with light of wavelength λ = 5000 Å, the distance between the slits is 0.2 mm and the screen is at 200 cm from the slits. The central maximum is at x = 0. The third maximum (taking the central maximum as zeroth maximum) will be at x equal to ______.
In a double-slit experiment, green light (5303 Å) falls on a double slit having a separation of 19.44 µ-m and a width of 4.05 µm. The number of bright fringes between the first and the second diffraction minima is ______.
In a double slit interference experiment, the distance between the slits is 0.05 cm and screen is 2 m away from the slits. The wavelength of light is 6000 Å. The distance between the fringes is ______.
In a biprism experiment, the slit is illuminated by red light of wavelength 6400 A and the crosswire of eyepiece is adjusted to the centre of 3rd bright band. By using blue light it is found that 4th bright band is at the centre of the cross wire. Calculate the wavelength of blue light.
