Advertisements
Advertisements
प्रश्न
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
पर्याय
3 : 4
4 : 3
9 : 16
16 : 9
उत्तर
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is 16 : 9.
Explanation:
Let the radii of the two spheres are r1 and r2, respectively.
∴ Volume of the sphere of radius,
r1 = V1 = `4/3 pi"r"_1^3` ...(i) [∵ Volume of sphere = `4/3pi` (radius)3]
And volume of the sphere of radius,
r2 = V2 = `4/3 pi"r"_2^3` ...(ii)
Given, ratio of volumes = V1 : V2 = 64 : 27
⇒ `(4/3 pi"r"_1^3)/(4/3 pi"r"_2^3) = 64/27` ...[Using equations (i) and (ii)]
⇒ `("r"_1^3)/("r"_2^3) = 64/27`
⇒ `"r"_1/"r"_2 = 4/3` ...(iii)
Now, ratio of surface area = `(4 pi"r"_1^2)/(4 pi"r"_2^2)` ...[∵ Surface area of a sphere = 4π (radius)2]
= `"r"_1^2/"r"_2^2`
= `("r"_1/"r"_2)^2`
= `(4/3)^2` ...[Using equation (iii)]
= 16 : 9
Hence, the required ratio of their surface area is 16 : 9.
APPEARS IN
संबंधित प्रश्न
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (use `pi=22/7`)
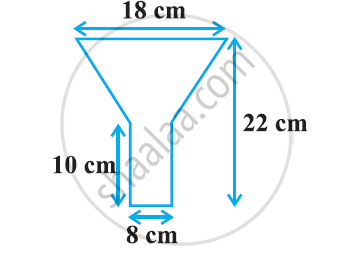
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
In a rain-water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3·5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use : π = 355/115)
A spherical glass vessel has a cylindrical neck that is 7 cm long and 4 cm in diameter. The diameter of the spherical part is 21 cm. Find the quantity of water the vessel can hold.
A farmer connects a pipe of internal diameter 25 cm from a canal into a cylindrical tank in his field, which is 12 m in diameter and 2.5 m deep. If water flows through the pipe at the rate of 3.6 km/hr, then in how much time will the tank be filled? Also, find the cost of water if the canal department charges at the rate of ₹ 0.07 per m3.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If its volume is 1617 cm3, the total surface area of the cylinder is
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
The surface areas of two spheres are in the ratio 1 : 2. The ratio of their volume is ______.
A bicycle wheel makes 500 revolutions in moving 1 km. Find the diameter of the wheel.
