Advertisements
Advertisements
प्रश्न
When the length of each side of a cube is increased by 3 cm, its volume is increased by 2457 cm3. Find its side. How much will its volume decrease, if the length of each side of it is reduced by 20%?
उत्तर
Let a be the side of the cube.
Side of the new cube = a + 3
Volume of the new cube = a3 + 2457
That is, ( a + 3 )3 = a3 + 2457
⇒ a3 + 3 x a x 3 ( a + 3 ) + 33 = a3 + 2457
⇒ 9a2 + 27a + 27 = 2457
⇒ 9a2 + 27a - 2430 = 0
⇒ a2 + 3a - 270 = 0
⇒ a ( a + 18 ) - 15 ( a + 18 ) = 0
⇒ ( a - 15 ) ( a + 18 ) = 0
⇒ a - 15 = 0 or a + 18 = 0
⇒ a = 15 or a = - 18
⇒ a = 15 cm ...[ since side cannot be negative ]
Volume of the cube whose side is 15 cm = 153 = 3375 cm3
Suppose the length of the given cube is reduced by 20%.
Thus new side a new = a - `20 / 100` x a
= `a ( 1 - 1/5)`
= ` 4/5` x 15
= 12 cm
Volume of the new cube whose side is 12 cm = 123 = 1728 cm3
Decrease in volume = 3375 - 1728 = 1647 cm3
APPEARS IN
संबंधित प्रश्न
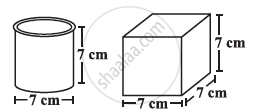
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
Find the surface area of a cube whose edge is 3 cm.
Find the surface area of a cube whose edge is 6 m .
Cubes A, B, C having edges 18 cm, 24 cm and 30 cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
The edges of three solid cubes are 6 cm, 8 cm, and 10 cm. These cubes are melted and recast into a single cube. Find the edge of the resulting cube.
Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.
The base of a rectangular container is a square of side 12 cm. This container holds water up to 2 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 224 cm3 of water overflows. Find the volume and surface area of the cube.
A cubical container of side 6.5 m is to be painted on the entire outer surface. Find the area to be painted and the total cost of painting it at the rate of ₹ 24 per m2
The total surface area of a cube is 96 cm2. The volume of the cube is ______.
