Question

Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:

 x + y = 5, 2x + 2y = 10

Answer 1

x + y = 5

2x + 2y = 10

`a_1/a_2=1/2, b_1/b_2=1/2, c_1/c_2 = (-5)/-10 =1/2`

Since `a_1/a_2=b_1/b_2=c_1/c_2`

Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.

x + y = 5

x = 5 - y

x	5	4	3
y	0	1	2

2x + 2y = 10

⇒ x + y = 5

x = 5 - y

By keeping the values of y as 0, 1, and 2, the values of x are obtained as 5, 4 and 3, respectively.

x	5	4	3
y	0	1	2

Hence, the graphic representation is as follows.

Graph for the equations x + y = 5 and 2x + 2y = 10

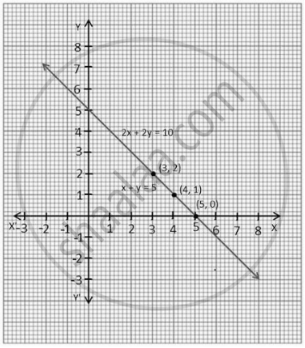
From the figure, it can be observed that these lines are overlapping each other. Therefore, infinite solutions are possible for the given pair of equations.