Advertisements
Advertisements
प्रश्न
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for the equation.
x2 – 9 = 13
उत्तर
x2 – 9 = 13
\[\Rightarrow x^2 - 9 - 13 = 0\]
\[ \Rightarrow x^2 - 22 = 0\]
\[ \Rightarrow x^2 + 0x - 22 = 0\]
So, it is of the form ax2 + bx + c = 0 where a = 1, b = 0 and c = −22.
APPEARS IN
संबंधित प्रश्न
(a) `3x-x^2=x^2+5` (b) `(x+2)^2=2(x^2-5)`
(c) `(sqrt2x+3)^2=2x^2+6` (d)` (x-1)^2=3x^2+x-2`
If the equation `x^2+5kx+16=0` has no real roots then
(a)`k>8/5` (b) `k(-8)/5`
(c)` (-8)/5<k<8/5` (d) None Of these
The perimeter of a rectangle is 82m and its area is `400m^2` . The breadth of the rectangle is
(a) 25m (b)20m
(c) 16m (d)9m
The sum of two natural numbers is 8 and their product is 15., Find the numbers.
Find the roots of the quadratic equation `2x^2-x-6=0`
If the roots of the quadratic equation `px(x-2)+=0` are equal, find the value of p.
Solve` 4sqrt3x^2+5x-2sqrt3=0`
If 1 is a root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0 then ab equals: ?
Write any two quadratic equations.
Decide whether the following equation is quadratic equation or not.
m3 + 3m2 – 2 = 3m3
Vivek is older than Kishor by 5 years. The sum of the reciprocals of their ages is \[\frac{1}{6}\] Find their present ages.
Choose the correct answer for the following question.
\[\sqrt{5} m^2 - \sqrt{5}m + \sqrt{5} = 0\] which of the following statement is true for this given equation?
If 3x + 5y = 9 and 5x + 3y = 7 find the value of x + y.
Solve any four of the following.
Find the value of y in the equation x + y = 12, when x = 5
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for equation.
P(3+6p) = –5
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Write the degree of Polynomial 5x2 + 2x + 3x4 + 4.
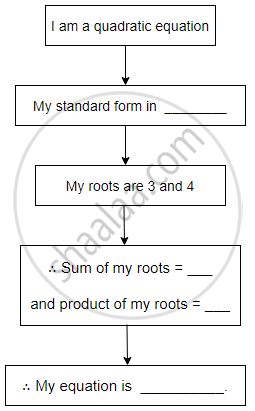
Complete the following activity to form a quadratic equation.
Activity:
Find the value of k for which the quadratic equation kx (x − 2) + 6 = 0 has two equal roots.
In a right-angled triangle, altitude is 2 cm longer than its base. Find the dimensions of the right-angled triangle given that the length of its hypotenuse is 10 cm.
