Advertisements
Advertisements
प्रश्न
Write the solution set of the inequation \[\left| \frac{1}{x} - 2 \right| > 4\]
उत्तर
\[\text{ We have }: \]
\[\left| \frac{1}{x} - 2 \right| > 4\]
\[\text{ Here, two cases arise } . \]
\[\text{ CASE 1: When } \frac{1}{x} - 2 > 0, \text{ then } \left| \frac{1}{x} - 2 \right| = \frac{1}{x} - 2\]
\[ \therefore \frac{1}{x} - 2 > 4\]
\[ \Rightarrow \frac{1}{x} - 2 - 4 > 0\]
\[ \Rightarrow \frac{1}{x} > 6\]
\[ \Rightarrow x \in \left( 0, \frac{1}{6} \right) . . . (i)\]
\[\text{ CASE 2: When } \frac{1}{x} - 2 < 0, \text{ then } \left| \frac{1}{x} - 2 \right| = - \left( \frac{1}{x} - 2 \right)\]
\[ \therefore - \frac{1}{x} + 2 > 4\]
\[ \Rightarrow - \frac{1}{x} > 2\]
\[ \Rightarrow \frac{1}{x} < - 2\]
\[ \Rightarrow x \in \left( - \infty , \frac{- 1}{2} \right) . . . (ii)\]
\[\text{ Hence, the solution set of the given inequation is the union of (i) and (ii) }. \]
\[ \therefore x \in \left( - \infty , \frac{- 1}{2} \right) \cup \left( 0, \frac{1}{6} \right)\]
APPEARS IN
संबंधित प्रश्न
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically: 2x – y > 1, x – 2y < –1
Solve the following system of inequalities graphically: x + y ≤ 6, x + y ≥ 4
Solve the following system of inequalities graphically: 2x + y≥ 8, x + 2y ≥ 10
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: 2x + y≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solve the following system of inequalities graphically: x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Find all pairs of consecutive odd positive integers, both of which are smaller than 10, such that their sum is more than 11.
Find all pairs of consecutive odd natural number, both of which are larger than 10, such that their sum is less than 40.
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
To receive grade 'A' in a course, one must obtain an average of 90 marks or more in five papers each of 100 marks. If Shikha scored 87, 95, 92 and 94 marks in first four paper, find the minimum marks that she must score in the last paper to get grade 'A' in the course.
A company manufactures cassettes and its cost and revenue functions for a week are \[C = 300 + \frac{3}{2}x \text{ and } R = 2x\] respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold for the company to realize a profit?
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 7.2 and 7.8. If the first two pH reading are 7.48 and 7.85, find the range of pH value for the third reading that will result in the acidity level being normal.
Write the solution set of the equation |2 − x| = x − 2.
Write the set of values of x satisfying the inequations 5x + 2 < 3x + 8 and \[\frac{x + 2}{x - 1} < 4\]
Write the solution set of the inequation |x − 1| ≥ |x − 3|.
Solve each of the following system of equations in R.
\[5x - 7 < 3\left( x + 3 \right), 1 - \frac{3x}{2} \geq x - 4\]
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Solve the following system of inequalities `(2x + 1)/(7x - 1) > 5, (x + 7)/(x - 8) > 2`
Find the linear inequalities for which the shaded region in the given figure is the solution set.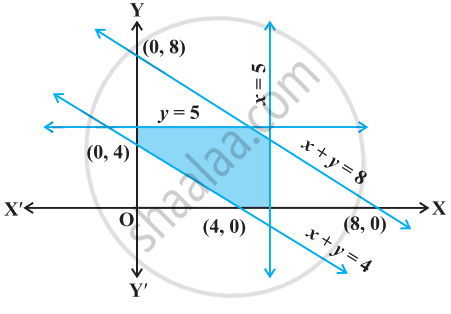
Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
Solution set of x ≥ 0 and y ≤ 1 is