Advertisements
Advertisements
प्रश्न
Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
उत्तर
We have, 3x + 2y ≥ 24,
3x +y ≤ 15, x ≥ 4
Now let’s plot lines 3x + 2y = 24, 3x + y = 15 and x = 4 on the coordinate plane.
Line 3x + 2y = 24 passes through the points (0, 12) and (8, 0).
Line 3x+y = 15 passes through points (5, 0) and (0, 15).
Also line x = 4 is passing through the point (4, 0) and vertical.
For (0, 0), 3(0) + 2(0) – 24 < 0.
Therefore, the region satisfying the inequality 3x + 2y ≥ 24 and (0, 0) lie on the opposite of the line 3x + 2y = 24.
For (0), 3(0) + (0) – 15 ≤ 0.
Therefore, the region satisfying the inequality 3x +y ≤ 15 and (0,0) lie on the same side of the line 3x +y = 15.
The region satisfying x ≥ 4 lies to the right-hand side of the line x = 4.
These regions are plotted as shown in the following figure
It is clear from the graph that there is no common region corresponding to these inequalities.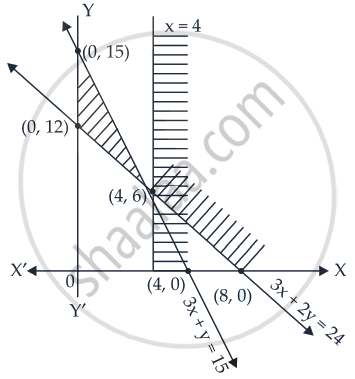
Hence, the given system of inequalities has no solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically: 2x + y≥ 8, x + 2y ≥ 10
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solve the following system of inequalities graphically: x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Find all pairs of consecutive odd natural number, both of which are larger than 10, such that their sum is less than 40.
Find all pairs of consecutive even positive integers, both of which are larger than 5, such that their sum is less than 23.
To receive grade 'A' in a course, one must obtain an average of 90 marks or more in five papers each of 100 marks. If Shikha scored 87, 95, 92 and 94 marks in first four paper, find the minimum marks that she must score in the last paper to get grade 'A' in the course.
A company manufactures cassettes and its cost and revenue functions for a week are \[C = 300 + \frac{3}{2}x \text{ and } R = 2x\] respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold for the company to realize a profit?
The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 7.2 and 7.8. If the first two pH reading are 7.48 and 7.85, find the range of pH value for the third reading that will result in the acidity level being normal.
Write the solution set of the equation |2 − x| = x − 2.
Write the set of values of x satisfying |x − 1| ≤ 3 and |x − 1| ≥ 1.
Write the solution set of the inequation \[\left| \frac{1}{x} - 2 \right| > 4\]
Write the number of integral solutions of \[\frac{x + 2}{x^2 + 1} > \frac{1}{2}\]
Write the set of values of x satisfying the inequations 5x + 2 < 3x + 8 and \[\frac{x + 2}{x - 1} < 4\]
Write the solution of set of\[\left| x + \frac{1}{x} \right| > 2\]
Write the solution set of the inequation |x − 1| ≥ |x − 3|.
Solve the following system of inequalities graphically.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Solve the following system of inequalities `(2x + 1)/(7x - 1) > 5, (x + 7)/(x - 8) > 2`
Show that the following system of linear inequalities has no solution x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
