Advertisements
Advertisements
प्रश्न
Solve the following system of inequalities graphically.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
उत्तर
To find graphical solution, construct the table as follows:
| Inequation | Equation | Double Intercept form | Points (x, y) | Region |
| 3x + 2y ≤ 12 | 3x + 2y = 12 | A (4, 0), B (0, 6) |
3(0) + 2(0) ≤ 12 ∴ 0 ≤ 12 ∴ origin side |
|
| x ≥ 1 | x = 1 | – | – | 0 ∴ R.H.S. of line x = 1 |
| y ≥ 2 | y = 2 | – | – | 0 ∴ above line y = 2 |
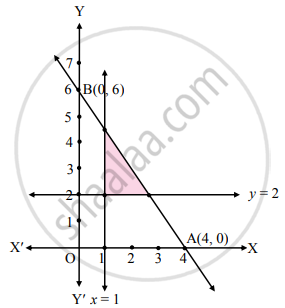
The shaded portion represents the graphical solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically: 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Find all pairs of consecutive odd natural number, both of which are larger than 10, such that their sum is less than 40.
Find all pairs of consecutive even positive integers, both of which are larger than 5, such that their sum is less than 23.
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
To receive grade 'A' in a course, one must obtain an average of 90 marks or more in five papers each of 100 marks. If Shikha scored 87, 95, 92 and 94 marks in first four paper, find the minimum marks that she must score in the last paper to get grade 'A' in the course.
The longest side of a triangle is three times the shortest side and third side is 2 cm shorter than the longest side if the perimeter of the triangles at least 61 cm, find the minimum length of the shortest-side.
Write the number of integral solutions of
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Solution set of x ≥ 0 and y ≤ 0 is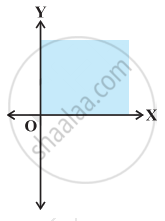
Solution set of x ≥ 0 and y ≤ 1 is