Advertisements
Advertisements
प्रश्न
यदि (– 4, 3) और (4, 3) एक समबाहु त्रिभुज के दो शीर्ष हैं, तो इस त्रिभुज के तीसरे शीर्ष के निर्देशांक ज्ञात कीजिए, जब कि दिया है कि मूलबिंदु त्रिभुज के अभ्यंतर में स्थित है।
उत्तर
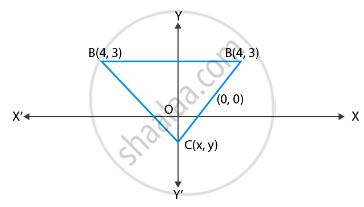
माना कि शीर्ष (x, y) हैं।
(x, y) और (4, 3) के बीच की दूरी = `sqrt((x - 4)^2 + (y - 3)^2)` ...(1)
(x,y) और (– 4, 3) के बीच की दूरी = `sqrt((x + 4)^2 + (y - 3)^2)` ...(2)
(4, 3) और (– 4, 3) के बीच की दूरी = `sqrt((4 + 4)^2 + (3 - 3)^2) = sqrt(8)^2`= 8
प्रश्न के अनुसार,
समीकरण (1) = (2)
(x – 4)2 = (x + 4)2
x2 – 8x + 16 = x2 + 8x + 16
16x = 0
x = 0
साथ ही, समीकरण (1) = 8
(x – 4)2 + (y – 3)2 = 64 ...(3)
x का मान (3) में प्रतिस्थापित करने पर
फिर (0 – 4)2 + (y – 3)2 = 64
(y – 3)2 = 64 – 16
(y – 3)2 = 48
y – 3 = `(+)4sqrt(3)`
y = `3(+) 4sqrt(3)`
उपेक्षा y = `3(+) 4sqrt(3)` ऐसा है कि y = `3(+) 4sqrt(3)` तो मूल त्रिभुज का आंतरिक भाग नहीं हो सकता।
इसलिए, तीसरा शीर्ष = `(0, 3 - 4sqrt(3))`
APPEARS IN
संबंधित प्रश्न
मान लीजिए A (4, 2), B (6, 5) और C (1, 4) एक त्रिभुज ABC के शीर्ष हैं।
(i) A से होकर जाने वाली माध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित ऐसे बिंदु P के निर्देशांक ज्ञात कीजिए कि AP : PD = 2 : 1 हो।
(iii) माध्यिकाओं BE और CF पर ऐसे बिंदुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2 : 1 हो और CR : RF = 2 : 1 हो।
(iv) आप क्या देखते हैं?
(v) यदि A (x1, y1), B (x2, y2) और C (x3, y3) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केंद्रक के निर्देशांक ज्ञात कीजिए।
बिंदु (0, –7) स्थित है :
x-अक्ष पर स्थित सभी बिंदुओं की कोटि है :
वह बिंदु, जहाँ दोनों निर्देशांक अक्ष मिलते हैं, कहलाता है :
किसी बिंदु का भुज धनात्मक होता है :
y-अक्ष से बिंदु P(3, 4) की लांबिक दूरी है :
बिंदु (1, −1) और (−1, 1) एक ही चतुर्थांश में स्थित है।
उस बिंदु के निर्देशांक (2, 0) हैं जो y-अक्ष पर x-अक्ष से 2 मात्रक की दूरी पर स्थित है।
किस चतुर्थांश अथवा किस अक्ष पर निम्नलिखित बिंदु स्थित हैं?
(– 3, – 6)
बिंदु (-4, -3) किस चतुर्थांश में होगा?
