Advertisements
Advertisements
The graph of y = f(x) is shown in the figure for some polynomial f(x).
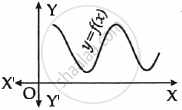
The number of zeroes of f(x) is ______.
Concept: Geometrical Meaning of the Zeroes of a Polynomial
Find a quadratic polynomial whose zeroes are 6 and – 3.
Concept: Relationship Between Zeroes and Coefficients of a Polynomial
Find the zeroes of the polynomial x2 + 4x – 12.
Concept: Relationship Between Zeroes and Coefficients of a Polynomial
Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream.
Concept: Pair of Linear Equations in Two Variables
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
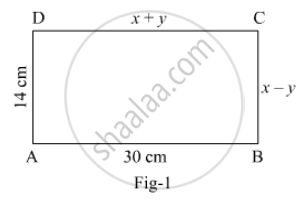
Concept: Equations Reducible to a Pair of Linear Equations in Two Variables
3 chairs and 1 table cost ₹ 900; whereas 5 chairs and 3 tables cost ₹ 2,100. If the cost of 1 chair is ₹ x and the cost of 1 table is ₹ y, then the situation can be represented algebraically as ______.
Concept: Algebraic Methods of Solving a Pair of Linear Equations > Substitution Method
Read the following passage:
|
A coaching institute of Mathematics conducts classes in two batches I and II and fees for rich and poor children are different. In batch I, there are 20 poor and 5 rich children, whereas in batch II, there are 5 poor and 25 rich children. The total monthly collection of fees from batch I is ₹9,000 and from batch II is ₹26,000. Assume that each poor child pays ₹x per month and each rich child pays ₹y per month.
|
Based on the above information, answer the following questions:
- Represent the information given above in terms of x and y.
- Find the monthly fee paid by a poor child.
OR
Find the difference in the monthly fee paid by a poor child and a rich child. - If there are 10 poor and 20 rich children in batch II, what is the total monthly collection of fees from batch II?
Concept: Pair of Linear Equations in Two Variables
Read the following passage:
Two schools 'P' and 'Q' decided to award prizes to their students for two games of Hockey ₹ x per student and Cricket ₹ y per student. School 'P' decided to award a total of ₹ 9,500 for the two games to 5 and 4 Students respectively; while school 'Q' decided to award ₹ 7,370 for the two games to 4 and 3 students respectively. |
Based on the above information, answer the following questions:
- Represent the following information algebraically (in terms of x and y).
- (a) What is the prize amount for hockey?
OR
(b) Prize amount on which game is more and by how much? - What will be the total prize amount if there are 2 students each from two games?
Concept: Algebraic Methods of Solving a Pair of Linear Equations > Elimination Method
A lending library has a fixed charge for first three days and an additional charge for each day thereafter. Rittik paid 27 for a book kept for 7 days and Manmohan paid ₹ 21 for a book kept for 5 days. Find the fixed charges and the charge for each extra day.
Concept: Pair of Linear Equations in Two Variables
Find the values of 'a' and 'b' for which the system of linear equations 3x + 4y = 12, (a + b)x + 2(a – b)y = 24 has infinite number of solutions.
Concept: Pair of Linear Equations in Two Variables
Read the following passage:
 Lokesh, a production manager in Mumbai, hires a taxi everyday to go to his office. The taxi charges in Mumbai consists of a fixed charges together with the charges for the distance covered. His office is at a distance of 10 km from his home. For a distance of 10 km to his office, Lokesh paid ₹ 105. While coming back home, he took another roµte. He covered a distance of 15 km and the charges paid by him were ₹ 155. |
Based on the above information, answer the following questions:
- What are the fixed charges?
- What are the charges per km?
- If fixed charges are ₹ 20 and charges per km are ₹ 10, then how much Lokesh have to pay for travelling a distance of 10 km?
OR
Find the total amount paid by Lokesh for travelling 10 km from home to office and 25 km from office to home. [Fixed charges and charges per km are as in (i) and (ii).
Concept: Pair of Linear Equations in Two Variables
If the quadratic equation px2 − 2√5px + 15 = 0 has two equal roots then find the value of p.
Concept: Nature of Roots of a Quadratic Equation
If `x=2/3` and x =−3 are roots of the quadratic equation ax2 + 7x + b = 0, find the values of a and b.
Concept: Nature of Roots of a Quadratic Equation
If x=−`1/2`, is a solution of the quadratic equation 3x2+2kx−3=0, find the value of k
Concept: Nature of Roots of a Quadratic Equation
Solve the quadratic equation 2x2 + ax − a2 = 0 for x.
Concept: Nature of Roots of a Quadratic Equation
Find the roots of the following quadratic equation by factorisation:
`sqrt2 x^2 +7x+ 5sqrt2 = 0`
Concept: Solutions of Quadratic Equations by Factorization
Find the value of k for which the equation x2 + k(2x + k − 1) + 2 = 0 has real and equal roots.
Concept: Nature of Roots of a Quadratic Equation
If the equation (1 + m2) x2 + 2mcx + c2 – a2 = 0 has equal roots then show that c2 = a2 (1 + m2)
Concept: Quadratic Equations
A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed. If it takes 3 hours to complete the total journey, what is the original average speed?
Concept: Quadratic Equations
The sum of two natural numbers is 15 and the sum of their reciprocals is `3/10`. Find the numbers.
Concept: Solutions of Quadratic Equations by Factorization

