Advertisements
Advertisements
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Concept: Number of Tangents from a Point on a Circle
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Concept: Tangent to a Circle
Prove that a parallelogram circumscribing a circle is a rhombus.
Concept: Number of Tangents from a Point on a Circle
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Concept: Number of Tangents from a Point on a Circle
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Concept: Similarity of Triangles
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Concept: Similarity of Triangles
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Concept: Similarity of Triangles
Prove that `sqrt(5)` is an irrational number.
Concept: Concept of Irrational Numbers
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Concept: Number of Tangents from a Point on a Circle
A motor boat whose speed in still water is 18 km/hr takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Concept: Solutions of Quadratic Equations by Completing the Square
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
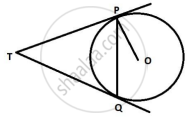
Concept: Concept of Circle
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
Concept: Number of Tangents from a Point on a Circle
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
Concept: Criteria for Similarity of Triangles
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
Concept: Heights and Distances
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
Concept: Heights and Distances
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
Concept: Area of Circle
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
Concept: Area of Circle
If the sum of first 7 terms of an A.P. is 49 and that of its first 17 terms is 289, find the sum of first n terms of the A.P.
Concept: Sum of First ‘n’ Terms of an Arithmetic Progressions
Prove that `(sin "A" - 2sin^3 "A")/(2cos^3 "A" - cos "A") = tan "A"`
Concept: Trigonometric Ratios
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
Concept: Heights and Distances
