Advertisements
Advertisements
Question
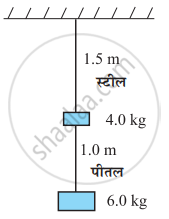
0.25 cm व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र के अनुसार भारित हैं। बिना भार लटकाए इस्पात तथा पीतल के तारों की लंबाइयाँ क्रमशः स्टील 1.5 m तथा 1.0 m हैं। यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः 20 × 1011 Pa तथा 0.91×1011 Pa हों तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।
Solution
यहाँ स्टील के तार के लिए
त्रिज्या r1 = (0.25/2) cm = 0.125 cm
= 0.125 × 10-2 m
लंबाई L1 = 1.5 m,
यंग-प्रत्यास्थता गुणांक `"Y"_1 = 2.0 xx 10^11` Pa
`= 2.0 xx 10^11 "N"//"m"^2`
भार `"F"_1 = 4.0 "kg" "भार" = 4.0 xx 9.8 "N" = 39.2 "N"`
∴ स्टील के लिए सूत्र - `"Y"_1 = ("F"_1"L"_1)/("A"_1"l"_1) = ("F"_1"L"_1)/(pi"r"_1^2"l"_1)` से,
स्टील की लंबाई में वृद्धि,
`"l"_1 = ("F"_1"L"_1)/(pi"r"_1^2"Y"_1)`
= `(39.2 "N" xx 1.5 "m")/(3.14 xx (0.125 xx 10^-2 "m")^2(2.0 xx 10^11 "N"//"m"^2))`
= `6 xx 10^-5 "m"`
यहाँ पितल के तार के लिए-
त्रिज्या `"r"_2 = "r"_1 = 0.125 xx 10^-2` m ; लंबाई L2 = 1.0 m
यंग-प्रत्यास्थता गुणांक `"Y"_2 = 0.91 xx 10^11 "Pa" = 0.91 xx 10^11 "N"//"m"^2`
भार F2 = (4 + 6.0) kg भार = 10 × 9.8 N = 98 N
∴ पीतल के लिए सूत्र `"Y"_2 = ("F"_2"L"_2)/("A"_1"l"_2) = ("F"_2"L"_2)/(pi"r"_2^2"l"_2)` से,
पीतल की लंबाई में वृद्धि,
`"l"_2 = ("F"_2"L"_2)/(pi"r"_2^2"Y"_2)`
= `(98 "N" xx 1.0 "m")/(3.14 xx (0.125 xx 10^-2 "m")^2 xx 0.91 xx 10^11 "N"//"m"^2)`
= `2.19 xx 10^-4` m
APPEARS IN
RELATED QUESTIONS
4.7 m लंबे व 3.0 x 10-5 m2 अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लंबे व 40 x 10-5m2 अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनकी लम्बाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग-प्रत्यास्थता गुणांकों में क्या अनुपात है?
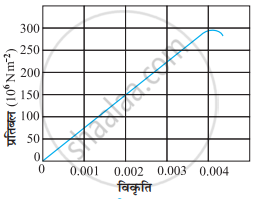
चित्र में किसी दिए गए पदार्थ के लिए प्रतिबल-विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए
- यंग-प्रत्यास्थता गुणांक, तथा
- सन्निकट पराभव सामर्थ्य क्या है?
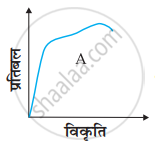
दो पदार्थों A और B के लिए प्रतिबल-विकृति ग्राफ चित्र में दर्शाए गए हैं।
 |
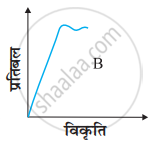 |
इन ग्राफों को एक ही पैमाना मानकर खींचा गया है।
- किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है?
- दोनों पदार्थों में कौन अधिक मजबूत है?
एक मीटर अतानित लंबाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँध कर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2 rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065cm2 है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिन्दु पर है।
