Advertisements
Advertisements
Question
10 पृथक पर्चियों पर 1 से 10 तक तक संख्याएँ लिखी हुई हैं (एक पर्ची पर संख्या), उन्हें एक बक्स में रखकर अच्छी प्रकार से मिला दिया जाता है। बक्स के अंदर से बिना देखे एक पर्ची निकली जाती है। निम्नलिखित की प्रायिकता क्या है?
- संख्या 6 प्राप्त करना।
- 6 से छोटी एक संख्या प्राप्त करना।
- 6 से बड़ी एक संख्या प्राप्त करना।
- 1 अंक की एक संख्या प्राप्त करना।
Solution
i. बॉक्स में 10 पर्चियाँ हैं। हालाँकि, 6 केवल 1 पर्ची पर लिखा है।
संख्या 6 प्राप्त करने की प्रायिकता = `1/10`
ii. 6 से छोटी संख्याएँ 1, 2, 3, 4 तथा 5 है। कुल 5 संख्याएँ है।
अतः 6 से छोटी संख्याएँ प्राप्त करने की प्रायिकता = `5/10 = 1/2`
iii. 6 से बड़ी संख्याएँ 7, 8, 9, 10 हैं।
6 से बड़ी संख्या प्राप्त होने की प्रायिकता = `4/10 = 2/5`
iv. 1 अंक की एक प्राप्त संख्या 9 हैं।अतः1, 2, 3, 4, 5, 6, 7, 8, 9 एक प्राप्त संख्या हैं।
1 अंक की एक प्राप्त संख्या = `9/10`
APPEARS IN
RELATED QUESTIONS
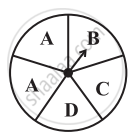
ज्ञात कीजिए D पर रुकने की प्रायिकता।
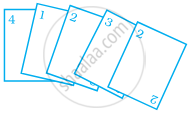
रोहन और शालू दी गई आकृति के अनुसार पाँच कार्डों से खेल रहे हैं। रोहन द्वारा इनमें से बिना देखे संख्या 2 लिखा हुआ कार्ड चुनने की प्रायिकता क्या है?
एक पासे को एक बार फेंकने पर, एक भाज्य संख्या प्राप्त करने की प्रायिकता `1/2` है।
एक प्रयोग के एक या अधिक परिणामों से एक घटना बनती है।
एक पासे को एक बार फेंकने पर संख्या 6 प्राप्त करने की प्रायिकता `1/6` है। इसी प्रकार, संख्या 5 प्राप्त करने की प्रायिकता `1/5` है।
एक पासे को एक बार फेंकने पर एक अभाज्य संख्या प्राप्त करने की प्रायिकता वही है, जो एक भाज्य संख्या प्राप्त करने की प्रायिकता है।
एक पासे को एक बार फेंका जाता है। इसकी क्या प्रायिकता है कि उस पर आने वाली संख्या होगी –
विषम
रितविक एक थैले में से, जिसमें सफेद और लाल गेंद हैं, एक गेंद निकालता है। एक सफेद् गेंद चुनने की प्रायिकता `2/9` है। यदि थैले में कुल 36 गेंद हैं, तो थैले में पीली गेंदों की संख्या ज्ञात कीजिए।
ताशों की गड्डी
ताशों की एक गड्डी में से निम्न काडों को निकाल कर उल्टा रख दिया जाता है –
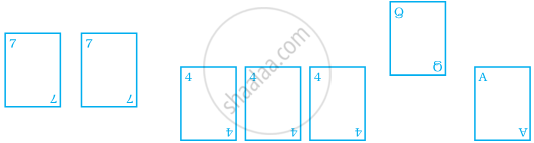
सुहेल जीत जाएगा, यदि वह एक फ़ेस (तस्वीर वाला) कार्ड चुनता है। सुहेल के जीतने की प्रायिकता ज्ञात कीजिए।
सोनिया नीचे दिए हुए कार्डों में से एक कार्ड चुनती है –

निम्न प्राप्त करने की प्रायिकता परिकलित कीजिए –
एक विषम संख्या
