Advertisements
Advertisements
Question
1000 tickets of a lottery were sold and there are 5 prizes on these tickets. If Namita has purchased one lottery ticket, what is the probability of winning a prize?
Solution
n(S) = 1000
n(E) = 5
P(E) = ?
P(E) = `"n(E)"/"n(S)" = 5/1000 = 0.005`.
APPEARS IN
RELATED QUESTIONS
The probability of an event that is certain to happen is ______. Such as event is called ______.
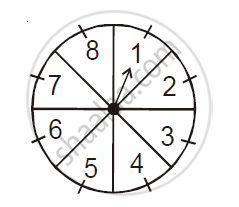
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the given figure), and these are equally likely outcomes. What is the probability that it will point at
- 8?
- an odd number?
- a number greater than 2?
- a number less than 9?
- A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
- Suppose the bulb drawn in (1) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the upper-most faces of two dice is between 5 and 8.
A card is drawn at random from a well-shuffled pack of 52 cards. Find the probability of getting
(i) a red king.
(ii) a queen or a jack.
Two dice are thrown at the same time. Find the probability of getting same number on both dice.
Cards with numbers 2 to 101 are placed in a box. A card is selected at random. Find the probability that the card has an even number
A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone if it is good but the trader will only buy a mobile if it has no major defect. One phone is selected at random from the lot. What is the probability that it is acceptable to Varnika?
Assertion (A): The probability that a leap year has 53 Sundays is `2/7`.
Reason (R): The probability that a non-leap year has 53 Sundays is `5/7`.
A bag contains 5 red balls and n green balls. If the probability of drawing a green ball is three times that of a red ball, then the value of n is ______.
