Advertisements
Advertisements
Question
- A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
- Suppose the bulb drawn in (1) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Solution
(i) Total number of bulbs = 20
∴ Total number of defective bulbs = 4
P (getting a defective bulb) = `4/20 = 1/5`
(ii) Remaining total number of bulbs = 20 − 1 = 19
Total number of possible outcome = 19
Remaining total number of non-defective bulbs = 16 − 1 = 15
∴ Number of favourable outcomes = 15
`"Number of favourable outcomes"/"Total number of possible outcomes" = 15/19`
P (getting a not defective bulb) = `15/19`
APPEARS IN
RELATED QUESTIONS
A die is numbered in such a way that its faces show the number 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws:
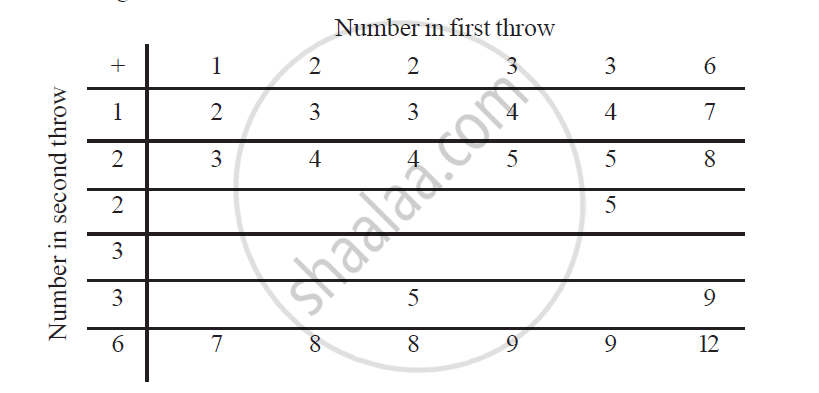
What is the probability that the total score is
(i) even? (ii) 6? (iii) at least 6?
A die is thrown. Find the probability of getting 2 or 4
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting the jack of hearts.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a king of red colour.
In a lottery there are 10 prizes and 25 blanks. What is the probability of getting a prize?
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is Red
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is Not black
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting a spade
In a class, there are 18 girls and 16 boys. The class teacher wants to choose one pupil for class monitor. What she does, she writes the name of each pupil on a card and puts them into a basket and mixes thoroughly. A child is asked to pick one card from the basket. What is the probability that the name written on the card is the name of a boy?
Fill in blank:
Probability of an event A + Probability of event ‘not A’ ...........
From a well-shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is a queen of black card.
20 tickets, on which numbers 1 to 20 are written, are mixed thoroughly and then a ticket is drawn at random out of them. Find the probability that the number on the drawn ticket is a multiple of 3 or 7 ?
Each card bears one letter from the word ‘mathematics’ The cards are placed on a table upside down. Find the probability that a card drawn bears the letter ‘m’.
If the probability of occurence of an event is p then the probability of non-happening of this event is (p − 1).
Two dice are thrown simultaneously. What is the probability that the sum of the numbers appearing on the dice is a prime number?
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. What is the probability that the card is a club?
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. What is the probability that the card is 10 of hearts?
At a fete, cards bearing numbers 1 to 1000, one number on one card, are put in a box. Each player selects one card at random and that card is not replaced. If the selected card has a perfect square greater than 500, the player wins a prize. What is the probability that the second player wins a prize, if the first has won?
The table given below shows the months of birth of 36 students of a class:
| Month of birth |
Jan. | Feb. | Mar. | Apr. | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
| No. of students |
4 | 3 | 5 | 0 | 1 | 6 | 1 | 3 | 4 | 3 | 4 | 2 |
A student is choosen at random. Fill in the boxes.
Total number of students = `square`
Let E be the event that the selected student is born in June.
Then,
Number of times event E occurs = `square`
So, P (selected student is born in June)
P(E) = `"Number of students born in June"/square`
= `square/square`
= `square`
Which of the following cannot be the probability of an event?
