Advertisements
Advertisements
Question
3x4 + 6x3 - 2x2 - 10x - 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक `sqrt(5/3)` और `-sqrt(5/3)` हैं।
Solution
दिया है : p(x) = 3x4 + 6x3 - 2x2 - 10x - 5
और दो शून्यक `sqrt(5/3)` और `-sqrt(5/3)` हैं।
अतः `x = sqrt(5/3), x = -sqrt(5/3)`
या `x - sqrt(5/3) = 0, x + sqrt(5/3) = 0`
या `(x - sqrt(5/3)) (x + sqrt(5/3)) = 0`
या `x^2 - (sqrt(5/3))^2 = 0`
या `x^2 - 5/3 = 0`
या 3x2 - 5 = 0
इसलिए, 3x2 - 5 p(x) का एक गुणनखंड है।
अब 3x2 - 5 से 3x4 + 6x3 - 2x2 - 10x - 5 में भाग देने पर
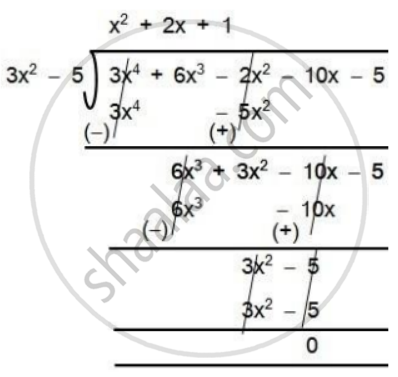
अतः p(x) = (3x2 - 5) (x2 + 2x + 1)
अब, x2 + 2x + 1 को गुणनखंड कर शून्यक ज्ञात करने पर -
= x2 + x + x + 1 = 0
= x(x + 1) + 1(x + 1) = 0
= (x + 1) (x + 1) = 0
या x + 1 = 0, x + 1 = 0
या x = -1, x = -1
अतः दो अन्य शून्यक -1 और -1 है।
APPEARS IN
RELATED QUESTIONS
विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए:
p(x) = x3 - 3x2 + 5x - 3, g(x) = x2 - 2
विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए:
p(x) = x4 - 3x2 + 4x + 5, g(x) = x2 + 1 - x
पहले बहुपद से दूसरे बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखंड है:
x2 + 3x + 1, 3x4 + 5x3 - 7x2 + 2x + 2
यदि x3 - 3x2 + x + 2 को एक बहुपद g(x) से भाग देने पर, भागफल और शेषफल क्रमशः x - 2 और -2x + 4 हैं तो g(x) ज्ञात कीजिए।
बहुपदों p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को संतुष्ट करते हों तथा घात r(x) = 0।
यदि बहुपद p(x) को बहुपद g(x) से भाग देने पर भागफल शून्य हो, तो p(x) और g(x) की घातों में क्या संबंध है?
यदि एक शून्येतर बहुपद p(x) को एक बहुपद g(x) से भाग देने पर शेषफल 0 हो, तो p(x) और g(x) की घातों में क्या संबंध है?
k का ऐसा मान ज्ञात कीजिए कि x2 + 2x + k बहुपद 2x4 + x3 – 14x2 + 5x + 6 का एक गुणनखंड हो जाए। इन दोनों बहुपदों के सभी शून्यक भी ज्ञात कौजिए।
a और b के किन मानों के लिए, q(x) = x3 + 2x2 + a के शून्यक बहुपद p(x) = x5 – x4 – 4x3 + 3x2 + 3x + b के भी शून्यक होंगे? p(x) के कौन से शून्यक q(x) के शून्यक नहीं है?
