Advertisements
Advertisements
Question
A 30 kg block is released from rest.If it slides down from a rough incline which is having co-efficient of friction 0.25.Determine the maximum compression of the spring.Take k=1000 N/m.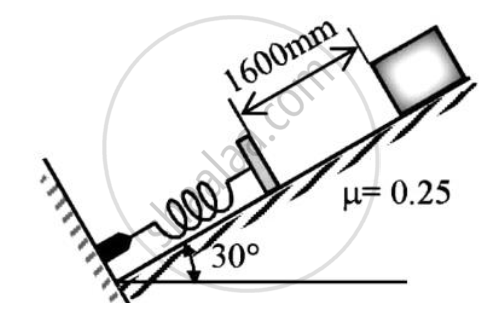
Solution
Given : Value of spring constant = 1000 N/m
W = 30N
μs = 0.25
To find : Maximum compression of the spring
Solution :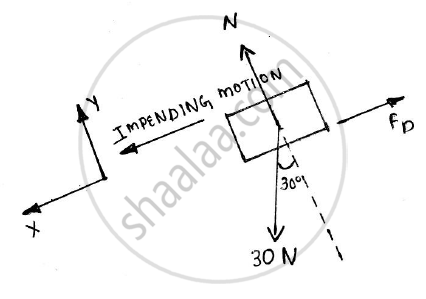
Let the spring be compressed by x cm when the box stops sliding
N = Wcos30
= 30 x 0.866
= 25.9808 N
Frictional force = μsN
= 0.25 x 25.9808
= 6.4952 N
Displacement of block = (1.6+x) m
Work done against frictional force = FD x s
=6.4952(1.6+x)
At position 1
v1=0 m/s
Vertical height above position(II) = h = (1.6+x) sin30
PE1 = mgh = 30(1.6+x)sin30 = 15(1.6+x)
KE1=`1/2`x mv12=0
Compression of spring=0
Initial spring energy = `1/2` x K x2 = 0
At position II
Assuming this position as ground position
H2 = 0
P.E2 = 0
Speed of block v = 0
K.E2 = `1/2` x mv2 = 0
Compression of spring = x
Final spring energy = ES = `1/2`x K x (x2)
= 0.5 x 1000 x x2
= 500x2
Appling work energy principle for the position (I) and (II)
U1-2 = KE2 - KE1
-WF + PE1 - PE2 - ES = KE2 - KE1
-6.4952(1.6+x) + 15(1.6+x)- 0- 500 x 2 = 0-0
500x2 - 8.5048x - 13.6077= 0
x=0.1737 m
The maximum compression of the spring is 0.1737 m
