Advertisements
Advertisements
Question
A battery of 9 V is connected in series with resistors of 0.2 Ω, 0.3 Ω, 0.4 Ω, 0.5 Ω and 12 Ω, respectively. How much current would flow through the 12 Ω resistor?
Solution
When equivalent resistances are connected in series,
R = R1 + R2 + R3 + R4 + R5
R1 = 0.2 Ω, R2 = 0.3 Ω, R3 = 0.4 Ω, R4 = 0.5 Ω, R5 = 12 Ω ....(Given)
R = 0.2 + 0.3 + 0.4 + 0.5 + 12
R = 13.4 Ω
V = IR ....(According to Ohm’s law)
I = `"V"/"R"`
= `9/13.4`
= 0.67 A
There will be no division of electric current because the resistors are connected in series.
0.67 A of electric current will flow in a 12 Ω resistor.
APPEARS IN
RELATED QUESTIONS
Find the expression for resistors connected in series.
A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio `"R"/"R'"` is ______.
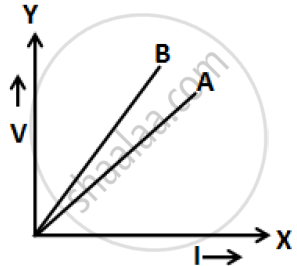
The V-I graph for a series combination and for a parallel combination of two resistors is shown in the figure below. Which of the two A or B. represents the parallel combination? Give reasons for your answer.
If the length of a wire is doubled by taking more of wire, what happens to its resistance?
A p.d. of 4 V is applied to two resistors of 6 Ω and 2 Ω connected in series. Calculate:
(a) the combined resistance
(b) the current flowing
(c) the p.d. across the 6 Ω resistor
The diagram below shows part of a circuit:
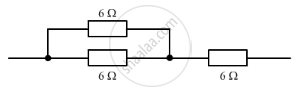
If this arrangement of three resistors was to be replaced by a single resistor, its resistance should be:
(a) 9 Ω
(b) 4 Ω
(c) 6 Ω
(d) 18 Ω
State how are the two resistors joined with a battery when same current flows in each resistor.
What is the equivalent resistance between A and B in the given circuit (Fig?)

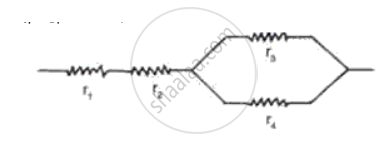
Calculate the equivalent resistance of the following combination of resistor r1, r2, r3, and r4
Write an expression for the resistance of a conducting wire in terms of its length and area of cross-section.
State expression for Cells connected in parallel.
What is a resistance? Define it with respect to Ohm’s law,
Calculate the equivalent resistance between the points A and B for the following combination of resistors:
2Ω resistor A, 1Ω resistor B and 4Ω resistor C are connected in parallel. The combination is connected across a 2V battery of negligible resistance. Draw the diagram of the arrangement and calculate:
(i) The current in each resistor A and C,
(ii) The current through battery.
With the help of a circuit diagram derive the formula for the resultant resistance of three resistances connected:
- in series and
- in parallel
Two wires of the same length and area made of two materials of resistivity ρ1 and ρ2 are connected in series to a source of potential V. The equivalent resistivity for the same area is:
Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of 4 Ω.
