Advertisements
Advertisements
Question
A battery of e.m.f 16 V and internal resistance 2 Ω is connected to two resistors 3Ω and 6Ω connected in parallel. Find:
- the current through the battery.
- p.d. between the terminals of the battery,
- the current in 3 Ω resistors,
- the current in 6 Ω resistor.
Solution
E.m.f. of battery E = 16V, r = 2Ω
Effective resistance of 3Ω and 6Ω connected in parallel R is
`1/"R" = 1/3 + 1/6`
= `3/6`
= `1/2`
∴ R = 2Ω
Total resistance = (R + r)
= (2 +2)
= 4Ω
(a) Current through battery
I = `"V"/("R" + r) = "E"/("R" +r)`
I = `(16V)/(4Ω)`
= 4 A
(b) p.d between terminal of battery
V = IR
= 4 × 2
= 8V
(c) The current in 3Ω resistor
I1 = `"V"/"R"`
= `8/3`
= 2.66 A
(d) The current in 6Ω resistor
I2 = `"V"/"R"`
= `8/6`
= 1.34 A
APPEARS IN
RELATED QUESTIONS
Differentiate between resistances in series and parallel.
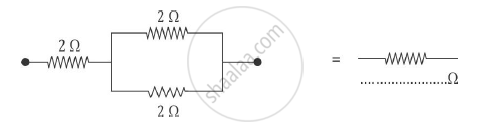
Complete the following :-
(c)
A resistor has a resistance of 176 ohms. How many of these resistors should be connected in parallel so that their combination draws a current of 5 amperes from a 220 volt supply line?
A wire of resistance R1 is cut into five equal pieces. These five pieces of wire are then connected in parallel. If the resultant resistance of this combination be R2, then the ratio `R_1/R_2` is:
(a) `1/25`
(b)1/5
(c)5
(c)25
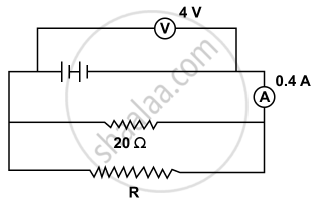
In the following figure calculate:
- the total resistance of the circuit
- the value of R, and
- the current flowing in R.
A uniform wire with a resistance of 27 Ω is divided into three equal pieces and then they are joined in parallel. Find the equivalent resistance of the parallel combination.
What are the advantages of a parallel connection?
Two resistors when connected in parallel give the resultant resistance of 2 ohms, but when connected in series the effective resistance becomes 9 ohms. Calculate the value of each resistance.
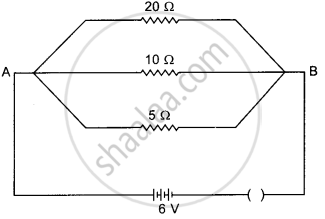
Calculate the current flows through the 10 Ω resistor in the following circuit.
A coil in the heater consumes power P on passing current. If it is cut into halves and joined in parallel, it will consume power:
